Vector Space To Word Analysis

데이터 분석을 진행할 때 데이터의 표현방식에 대한 공부가 중요하다는 생각으로 첫 포스팅을 텍스트 분석 시 word의 vectorize 방식으로 시작하게 되었습니다.

단어를 굳이 벡터 공간으로 옮기는 이유는 단어를 분석 가능한 형태로 바꾸기 위해서입니다. 즉 어떤 방식이던 해당 단어를 벡터 상 특정지을 수 있다면 어떤 공간이던간에 상관이 없다는 말이죠. 그래서 전 Word2Vec 등 단어 혹은 문서 등을 벡터로 변형시키는 방법(Vectorize)에 대해 공부하고자 포스팅을 시작합니다.

Bag of Words

Bag of Words, one-hot Representation이라고 불리는 방식은 간단하면서 기본적인 방식입니다. 하지만 강력한 효율을 가지고 있기에 꼭 알아야 하는 방식이고 방식은 단순히 문장에서 단어의 개수를 해당 위치에 넣어주는 방식 입니다.

즉, ( 문장 수 , 전체 단어 수 ) 와 같은 형태를 가진 행렬이 존재하고 (x,y)가 x문장에 y단어가 얼마나 등장했는가를 나타내는 2차원 행렬로 만드는 것입니다. 여기서 Bag of Words의 차원은 중복을 제외한 전체 단어 수임을 알 수 있습니다.

이러한 등장하는 빈도만을 고려한 방식이 어떻게 효율적일 수 있는가는 우리가 분석하는 개체가 텍스트이기 때문입니다. 텍스트 분석은 상당한 부분을 빈도수에 의존합니다. 얻을 수 있는 정보가 컴퓨터 비전에서의 이미지 정보들과 정형화 된 데이터들과는 다르게 거의 대부분의 데이터가 독립적이기 때문이라고 개인적으로 생각합니다.

그래서 이러한 문장을 빈도수를 위주로 표현해주기만 하더라도 어느정도의 효율을 얻을 수 있습니다.

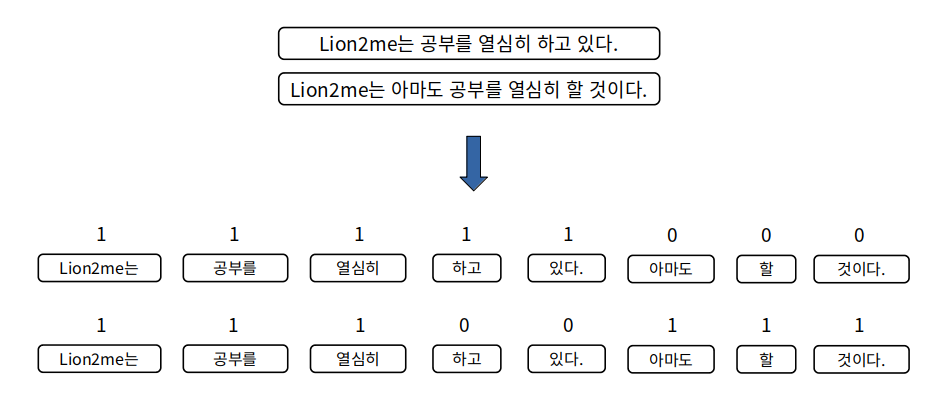
그림과 같이 문장을 Bag of Words로 벡터화 시키면 단어로 나누어 각각의 갯수를 세어 행렬 형태로 만들어주면서 SparseMatrix 형태가 만들어집니다.

SparseMatrix는 위 그림의 1) 아마도, 할, 것이다. 2) 하고, 있다. 와 같이 해당 문장에 없는 단어를 나타내는 위치에 0이 들어가는, 즉 실제 데이터가 희박한(Sparse) 행렬을 말합니다.

데이터가 많아질수록 실제로 벡터 안에 들어가는 단어의 수보다 전체 단어의 수는 늘어나고 그만큼 사용되지 않는 공간은 늘어나게 됩니다. 예시로는 2개의 문장을 사용했지만 10000개 이상의 문장을 분석하면 등장하는 단어의 종류에 비해 한 문장에 등장하는 단어는 극도로 적은 수임은 거의 확실합니다. 그래서 SparseMatrix는 메모리의 낭비라는 큰 문제점도 가지고 있습니다.

이런 점을 공부하며 직접 SparseMatrix를 만들어 주는 CountVectorizer를 구현 해보았습니다.

데이터는 국민청원 데이터를 사용했습니다. 국민청원 데이터는 청원 분류와 제목, 내용으로 이루어져있고, 이번 예제에서는 청원 제목을 SparseMatrix 형태로 만들어보겠습니다.

사용 방법은 DataFrame을 넣고 SparseMatrix 형태로 만들고자 하는 컬럼명을 인자로 넣으면 SparseMatrix 형태로 만들어주는 간단한 클래스입니다. SparseMatrix는 다음과 같은 여러가지 형태를 가질 수 있습니다.

# data = 국민청원 DataFrame
# title = DataFrame내 컬럼 명
# Rtype = coo , csr , csc 결과 리턴 형태
# n_gram = n_gram 범위

WTFV = WordToFrequencyVector(data)
BOW = WTFV.backOfWords('title',Rtype='csr',n_gram = (1,2))

• coo_matrix : A sparse matrix in COOrdinate format

• csr_matrix : Compressed Sparse Row matrix

• csc_matrix : Compressed Sparse Column matrix

• dok_matrix : Dictionary Of Keys based sparse matrix

• bsr_matrix : Block Sparse Row matrix

이 중에서 Sklearn의 CountVectorizer가 기본적으로 리턴하는 방식인 csr_matrix 방식을 기초로 coo_matrix 방식과 csc_matrix방식으로 리턴하도록 만들었습니다. 먼저 SparseMatrix 전체를 numpy.array() 형태로 리턴하는 coo_matrix형태로 데이터를 변환해보겠습니다.

위의 그림은 해당 데이터 중 10000개를 사용하여 coo_matrix 형태로 표현한 결과입니다.

국민청원 데이터는 약 45만개 단어의 수는 약 50만개로 coo_matrix 형태로 변환하면 약 45만 x 50만의 공간이 필요하기 때문에 메모리상의 크기 제한으로 Memory Error가 발생합니다. 이러한 경우를 방지하기 위해 csr_matrix 혹은 csc_matrix 방식이 자주 사용됩니다. 두 방식은 SparseMatrix를 행렬로 표현할 때 요소가 많을 경우 메모리의 사용량을 줄일 수 있는 방식으로 행과 열로 이루어져있는 특징을 이용해 (행, 열, 값) 혹은 (열, 행, 값)의 형태로 데이터를 표현하는 방식입니다.

최악으로 모든 요소에 모든 단어가 포함되어 있는 경우에는 45만 x 50만 x 3(행,열,값)의 메모리 사용이 더해질 수 있지만 SparseMatrix는 대부분의 요소가 0값을 가짐을 가정하기에 일반적으로 메모리 활용에 매우 효과적인 방법입니다.

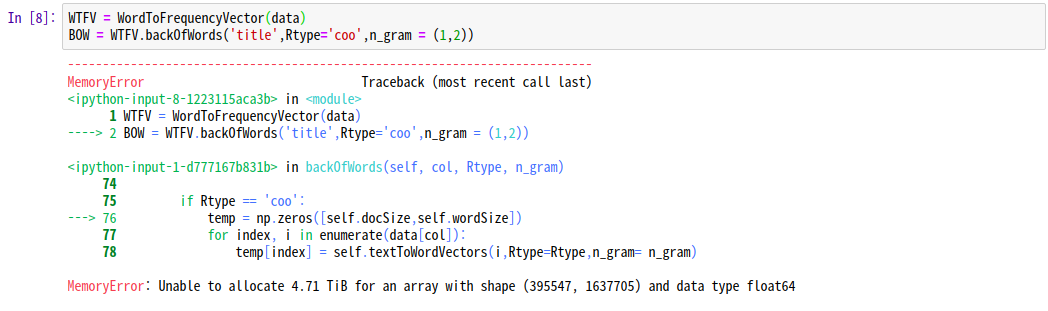
동일한 방식으로 coo_matrix 형태로 모든 데이터를 표현하려하면 다음과 같이 Memory Error가 발생하는 경우에도

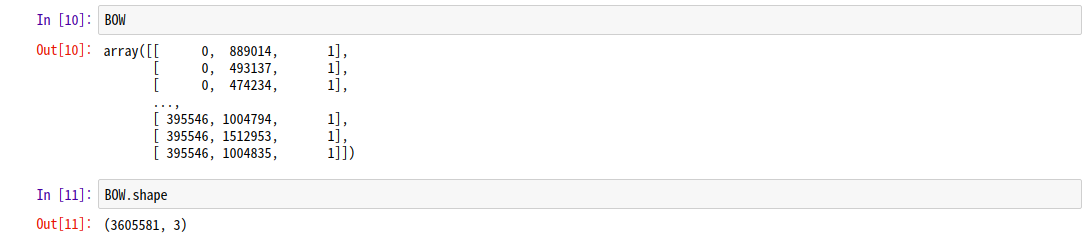
csr_matrix는 성공적으로 데이터를 표현할 수 있습니다.

이상으로 Bag of Words의 설명을 마치겠습니다.

Distributed Representation (Word2Vec)

이전에 공부한 Bag of Words의 방법은 텍스트 데이터를 벡터로 옮기는 방법이지만 각 벡터값이 의미하는 바는 단순히 “해당 문자열에 해당 단어가 몇 번 등장했다” 입니다. 이 정보로 분류 모델을 사용할 수 있습니다. 하지만 단어가 어떤 의미를 가지고 있는지, 비슷한 의미가 어떤 단어가 있는지를 알면 더욱 다양한 분야에 활용 할 수 있을 것 같습니다. 이런 의문에서 Distributed Representation 방식으로 단어를 표현하는 방법이 고안되었습니다.

Distributed Representation은 임베딩 벡터 공간을 임의로 만들어 각 단어를 설정한 차원의 벡터로 분산하여 표현하는 방법 이며 그런 단어 벡터를 이용하는 Word2Vec은 단어들의 함께 등장한 정보를 기반으로 유사한 단어들의 벡터를 모아주는 알고리즘 입니다.

Word2Vec의 아이디어

Word2Vec의 아이디어는 언어학의 Distributional Hypothesis를 기반으로 주변 단어들이 비슷한 형태를 띄고 있는 단어들은 비슷한 의미를 가지고 있지 않을까? 라는 질문에서 시작한 것으로 보여집니다. 예를 들면 이런 예를 들 수 있습니다.

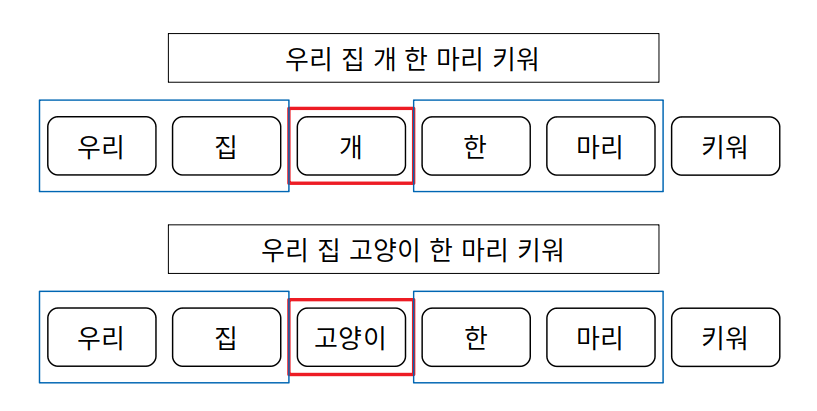
두 문장에 확인할 수 있는 정보는 개와 고양이는 유사한 정보를 가졌다고 볼 수 있습니다. 정확하게는 개와 고양이는 비슷한 특징이 존재하고, 그러므로 두 단어를 설명하는 주위 단어들은 유사한 형태를 가지고 있다. 라고 생각 할 수 있습니다.

예를 들어 고양이와 강아지의 벡터를 생각해보겠습니다.

3차원의 임베딩 벡터 공간에 “고양이”가 [0.9,0.7,0.9] 의 벡터를 가지고 “개”가 [0.5,0.3,0.7]의 벡터를 가지고 있다면 단순하게 다음과 같이 그릴 수 있습니다.

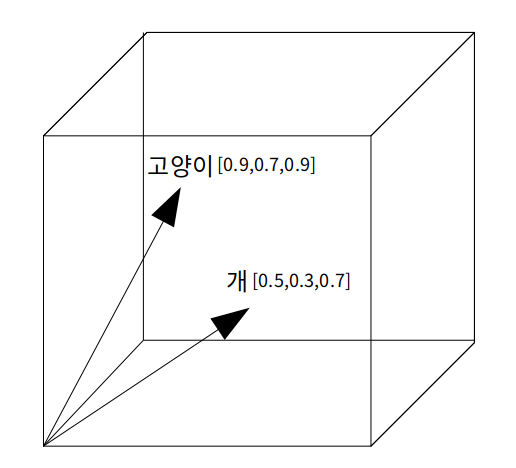
개와 고양이를 임베딩 벡터에 표현하는 것까지 성공했습니다. 이제 이 두 단어를 어떻게 비슷한 의미의 단어임을 알 수 있을까요? 답은 두 벡터가 비슷한 방향을 가리키면 비슷한 의미를 가진다고 가정하는 것입니다. 즉 두 벡터 사이의 거리를 기반으로 유사도를 측정하는 방식입니다. 그러면 우리는 두 벡터를 특정 방법을 이용하여 벡터를 가깝게 만들어 주면 됩니다. 그림 상에서는 두 가지 방법이 있습니다. 단순하게 고양이 벡터를 개 벡터 방향으로 이동시키거나 개 벡터를 고양이 벡터 방향으로 이동시키는 방법, 혹은 특정 한 방향으로 두 벡터를 모아주면 두 단어는 점점 유사한 벡터를 가지게 되는 것입니다. 이 부분에서 사용되는 알고리즘이 바로 Word2Vec입니다.

두 단어만으로는 관계성을 알 수 없으니 우리는 고양이와 개, 두 단어가 비슷한 의미를 가진다는 것을 주변 단어를 이용해서 알고자 했습니다. 그러니 정확한 그림은 이렇게 그릴 수 있습니다.

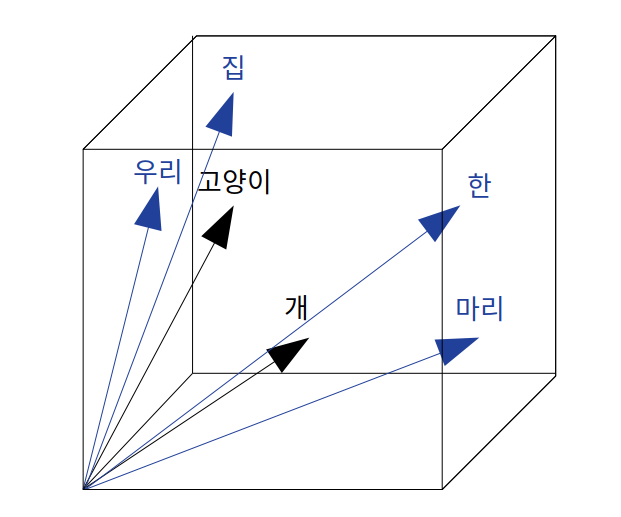
주변 단어들이 벡터에 생성되었으니 단순하게 고양이와 개 벡터를 주변 단어의 평균 벡터만으로 한번 이동시켜봅시다. 실제 알고리즘은 평균이 아닙니다.

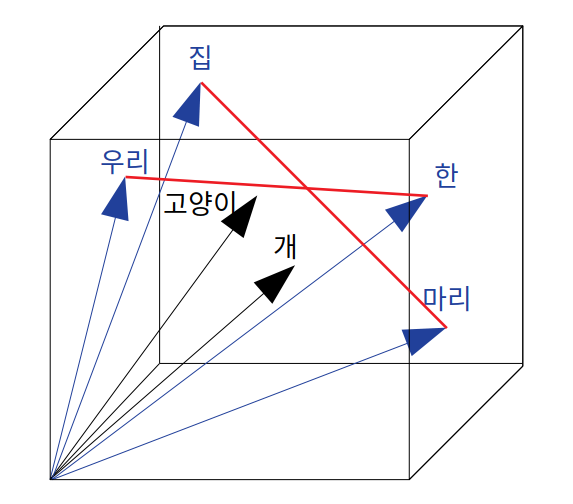
고양이 벡터도 개 벡터도 모두 비슷한 방향으로 벡터를 옮긴 것을 볼 수 있습니다. 실제 Word2Vec에서는 주변 단어도 벡터 상 이동을 거치며 이외에도 다양한 알고리즘을 사용하고있지만, 이후에 설명하겠습니다.

장점

간단한 벡터 평균으로 해당 단어를 이끌어오는 단순한 작업에서도 알 수 있듯이 Word2Vec의 단어 하나 내부의 벡터값 각각은 특정한 의미를 가지고 있지 않지만, 결국 벡터가 비슷한 단어들은 어느정도 비슷한 정보를 가짐을 유추할 수 있다는 점에서 각 단어의 특징이 포함 된 데이터가 되었음을 알 수 있습니다.

또한 각 벡터는 Sparse Representation과는 달리 0이 아닌 특정한 정보를 가지고 있다는 점에서 Distributed(Dense) Representation이라는 것을 알 수 있습니다. 그러므로 벡터 차원을 지나치게 크게 할당하지 않는 한 메모리 활용면에서도 효율적인 모델입니다. 예를 들면 Bag of Words 방식으로 국민청원 데이터를 벡터화 할 경우 45만(문장 수) * 50만(전체 단어 수)의 공간이 필요한 것에 비해 300차원의 임베딩 공간을 이용하여 데이터를 벡터화 할 경우 300(차원) * 50만(전체 단어 수)로 표현 할 수 있습니다.

이렇듯 Word2Vec을 이용하면 유사한 정보를 가진 정보를 어느정도 얻어 낼 수 있으며 단어를 표현하는 공간을 절약할 수 있는 장점이 있습니다.

Word2Vec 방식

Word2Vec은 설명을 듣고나면 지도 학습과 유사한 점이 있습니다. 주변 단어들의 벡터라는 정답이 있으며 어느정도의 답이 있는 상태에서 해당 답의 방향으로 벡터를 이동시키기 때문에 답이 존재하는 지도 학습과 유사하지만 Word2Vec은 비지도 학습 방식입니다. 별도의 학습이 없더라도 학습 데이터 안에 답이 있으며 그 정보를 이용하여 벡터를 바꿔주면 우리가 알고 싶은 고양이와 개가 유사한지에 대한 답을 얻을 수 있기 때문입니다.

Word2Vec은 크게 두 가지 방식을 사용합니다.

주변 단어로 단어를 유추하는 CBOW 방식과 단어로 주변 단어를 유추하는 Skip-Gram 방식이 있습니다.

1. CBOW

모든 환경은 embedding Vector 3 dimension으로 진행하겠습니다

CBOW 방식은 주변 단어로 단어를 유추하는 방식으로 다음과 같은 예시에서 빈칸을 예측해봅시다.

나는 뉴턴의 __ 처럼 사정없이 그녀에게로 굴러 떨어졌다.

첫사랑이 떠오르는 이 예시의 답은 “사과” 입니다. 우선 빈칸을 예측하고자 한다면 주변 단어를 살펴보아야 합니다. 주변 단어를 살펴보는 과정에서 Word2Vec은 window라는 파라미터를 제공합니다. 바로 주변 단어 중 몇 개를 볼 것인가를 정하는 파라미터로 window size를 2로 설정하면 예측하고자 하는 단어의 양 옆으로 2개를 살펴보는 것으로 총 4개의 주변 단어를 사용하게 됩니다.

일단 위의 문장에서 window = 2 기준으로 주변 단어를 살펴보면 나는, 뉴턴의, 처럼, 사정없이 라는 단어 셋이 나오게 됩니다.

주어진 단어의 주변 단어들로 해당 단어를 예측하는 방식을 천천히 따라가 보겠습니다. 문서 전체에 대해 단어 각각의 위치를 인덱싱하는 작업을 진행합니다. 이후 그 위치 정보를 기반으로 네트워크 상의 W(Input layer -> hidden layer)인 embedding Vector Table를 만듭니다. 그런 작업을 거치면 해당 단어를 One-Hot Encoding 만으로 해당 단어의 벡터를 구할 수 있게 됩니다. 그림으로 살펴보겠습니다.

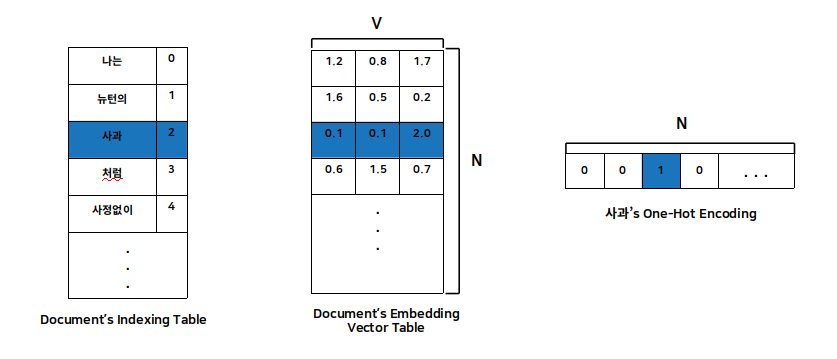
다음과 같이 데이터를 표현 할 준비가 되었다면 word2Vec을 적용시키는 일만 남았습니다. 현재 그림 속 파란색으로 표현 한 단어를 기반으로 CBOW 방식을 통해 학습을 진행하고 있습니다.

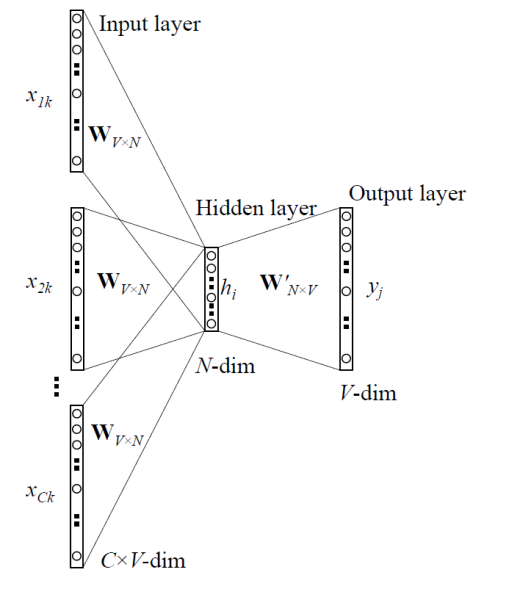
설명의 편의성을 위해 W’ 는 U로 표현하겠습니다.

그림에서 Input layer는 주어진 단어의 주변 단어들의 One-Hot encoding 값입니다. 여기서는 사과의 주변 단어의 One-Hot encoding 값을 구합니다.

이 값을 Embedding Vector Table (W)과 행렬곱을 하게 되면 바로 그 단어의 embedded Vector 값이 나오게 됩니다.

즉 이러한 과정은 단어의 embedded Vector로 변환하기 위한 단순한 Select 과정이라고 할 수 있습니다. 그림으로 보면 다음과 같습니다.

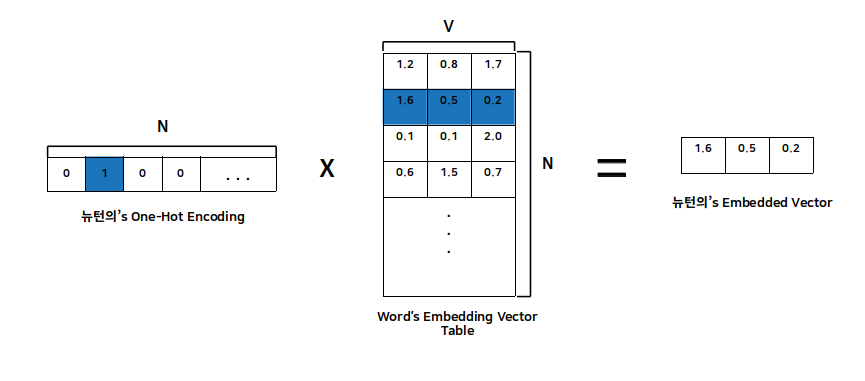
모든 단어가 Embedding Vector Table (W)을 거쳐서 각자 자신만의 Embedded Vector로 바꾼 후 모든 벡터를 더한 값을 WindowSize * 2를 나누어주어 평균을 구하면 바로 HiddenLayer의 값이 나옵니다.

그러므로 Output은 HiddenLayer에 대해 파라미터 U를 곱한 값입니다.

마지막으로 확률로 변환하기 위해 softmax를 사용하여 확률값으로 변환합니다.

이때 결과의 i 위치의 값은 예측하고자 하는 위치의 단어가 i 일 가능성을 나타내고 있습니다. 우리가 구하고 싶은 값은 주변 단어의 중심에 있는 값인 ‘사과’의 벡터이므로 해당 Output 값에서 ‘사과’에 위치한 값을 최대화, 즉 오차를 최소화 하는 방식을 사용하면 됩니다.

사용하는 최적화 기법은 SGD를 사용하고 Loss Function 은 다음과 같은 수식으로 나타 낼 수 있습니다.

여기서 y값이 OneHotVector이므로 예측하고자 하는 단어를 제외한 모든 값은 0이 곱해져 오차가 계산되지 않기 때문에 식을 단순화 시킬 수 있습니다. i를 예측 할 단어의 위치라고 생각하면 Loss는 다음과 같습니다.

\(y_i = Target\_Truth\) \(\hat y_i = Target\_Predict\) \(Loss = - y_ilog(\hat y_i)\)

최종적으로 모든 데이터에 대해 학습을 거치며 만들어진 W 는 그 자체가 Embedding Vector Space로 단어들의 유사도를 가진 공간이 됩니다.

이것으로 CBOW 방식에 대한 설명을 마칩니다. skip-gram에 관해서는 추후에 포스팅 하겠습니다.

참고 자료

• https://reniew.github.io/21/
• http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/
• https://dreamgonfly.github.io/blog/word2vec-explained/
• https://arxiv.org/abs/1411.2738