꾸준함이 중요한 Lion2me의 기술블로그

Sequential Models

20 Dec 2020
ML

Sequential Models

Sequential Models에서 Sequential한 데이터를 다룰 때 주로 사용되는 3가지의 모델에 대해 공부해보겠습니다. 그 3가지는 바로 Markov Model, Hidden Markov Model, Maximum Entropy Model, Maximum Entropy Markov Model, Conditional Random Field 입니다.

1. Markov Model

HMM, MEMM에서 등장하는 Markov Model부터 공부하겠습니다.

Markov Model를 저는 현재의 상태는 이전의 상태로부터 어느정도 영향을 받는다. 라고 이해했습니다.

우리는 날짜는 Sequential한 성질을 가지고 있음을 알고 있습니다. 예를들면 2021년 8월 20일의 기온을 2021년 8월 19일의 기온의 기준에서 보면 현재의 기온과 그리 차이가 나지 않는 기온임을 알 수 있습니다.

어떻게 표현하든 일단 Sequential한 데이터에서 이전의 관측값이 현재의 상태(State)에 영향을 주는 모델을 우리는 Marcov Model이라고 말 할 수 있습니다.

이전의 결과가 다음의 결과에 영향을 주는 모델을 Markov Model이라고 합니다. 단순 확률로 설명하면 다음과 같이 설명 할 수 있습니다.

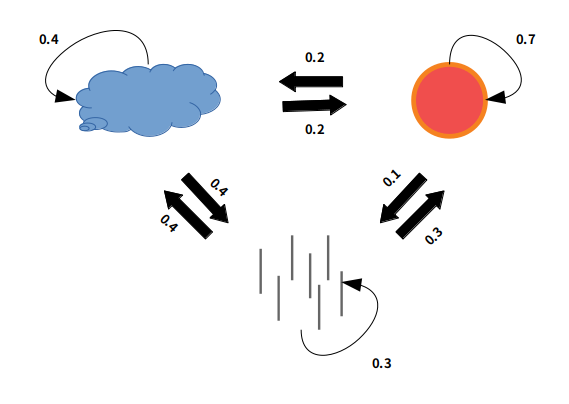
ex_screenshot

각 그림은 구름이 끼는 날, 해가 보이는 날, 비가 오는 날로 구분 된 정해진 확률분포입니다.

해가 뜨는 날의 다음 날 해가 뜰 확률은 70%이며 구름이 낄 확률은 20%, 비가 올 확률은 10% 라고 해석하시면 됩니다. 여기서 Marcov 모델을 적용시켜봅시다.

오늘 해가 떠 있으면 내일 해가 뜰 확률은 70%로써 Marcov 모델의 정의인 이전의 결과(관측값)이 이후의 결과값에 영향을 끼치는 것을 알 수 있습니다. 그럼 어제는 해가 뜬 날이고 연속으로 2일 동안 해가 뜰 확률을 찾으면 어떻게 될까요? 쉽게 알 수 있습니다.

\[0.7 * 0.7 = 0.49\]

하지만 이 연산이 가능 한 이유는 관측값을 알고있기 때문입니다. 현재 날씨가 맑다는 사실을 알고 있기 때문에 확률만 있으면 해당 사건이 일어날 확률을 구할 수 있는겁니다.

만약 현재 관측값이 없다면 어떻게 될까요?

여기서 Hidden Marcov Model을 시작할 수 있습니다.

2. Hidden Marcov Model

HMM은 쉽게 말하면 이전 관측값을 모르는(보여지지 않은) Marcov Model입니다. 이전의 관측값을 모르기 때문에 다음의 그림을 해석하는 방법은 조금 달라집니다.

ex_screenshot

어제의 날씨를 모를 때 우리는 오늘의 날씨의 확률을 구하고자 한다면 어떻게 구할 수 있을까요?

“어제 날씨는 모르겠지만 내일 해가 뜨면 좋겠다.”

일단 오늘 날씨를 모르기에 모든 날씨의 가정해봅니다. 가장 먼저 어제 구름이 낀 날씨라고 가정합니다.

구름 낀 날에서 2일 뒤의 해가 뜰 확률을 구합니다.

  • 구름 낀 날 - 구름 낀 날 - 해 뜬 날 = 0.4 * 0.2 = 0.08

  • 구름 낀 날 - 해 뜬 날 - 해 뜬 날 = 0.2 * 0.7 = 0.14

  • 구름 낀 날 - 비 온 날 - 해 뜬 날 = 0.4 * 0.3 = 0.12

결국 어제 구름 낀 날이라면 내일 해가 뜰 확률은 결국 34% 입니다. 결국 세 확률을 더하는 값이 내일 해가 뜰 확률이 되기 때문이죠.

마찬가지로 어제 해가 떴다면

  • 해 뜬 날 - 구름 낀 날 - 해 뜬 날 = 0.2 * 0.2 = 0.04

  • 해 뜬 날 - 해 뜬 날 - 해 뜬 날 = 0.7 * 0.7 = 0.49

  • 해 뜬 날 - 비 온 날 - 해 뜬 날 = 0.1 * 0.3 = 0.03

어제 해 뜬 날이라면 내일 해가 뜰 확률은 56% 입니다.

비가 온 날이였다면

  • 비 온 날 - 구름 낀 날 - 해 뜬 날 = 0.4 * 0.2 = 0.08

  • 비 온 날 - 해 뜬 날 - 해 뜬 날 = 0.3 * 0.7 = 0.21

  • 비 온 날 - 비 온 날 - 해 뜬 날 = 0.3 * 0.3 = 0.09

어제 비 온 날이라면 내일 해가 뜰 확률은 38% 입니다.

모든 확률을 더하면 1이 넘는 확률이 나옵니다. 말이 안되는 확률이죠. 이런 결과가 나온 이유는 우리가 시작한 날의 확률을 1로 잡았기 때문입니다. 예를 들어 구름 낀 날에서 시작해서 2일 뒤 해가 뜰 확률을 구할 때 우리는 현재 상태를 구름 낀 날 로 확정 지었습니다. 그러니 정확한 식은 다음과 같습니다.

  • 구름 낀 날 - 구름 낀 날 - 해 뜬 날 = 1 * 0.4 * 0.2 = 0.08

여기서 우리는 HMM의 중요한 파라미터인 initial 값을 지정해주어야 한다는 사실을 알 수 있습니다.

사전 확률을 지정하는 것과 유사합니다. 즉 우리는 비가 오는 날은 해가 뜨는 날과 구름 낀 날보다 적다는 사실을 알고 있습니다. 가장 일반적인 방법은 이전 1년의 기후를 기반으로 확률을 나타내는 방법도 있겠네요. 일단 임의의 initial 값을 사용해봅시다.

  • 어제 구름이 낀 확률은 0.4

  • 어제 해가 뜬 확률은 0.4

  • 어제 비가 왔을 확률은 0.2

그럼 다음의 사전확률을 기반으로 내일 해가 뜰 확률은 다음의 값을 더하면 됩니다.

  • 구름 낀 날 - 구름 낀 날 - 해 뜬 날 = 0.4 * 0.4 * 0.2 = 0.032

  • 구름 낀 날 - 해 뜬 날 - 해 뜬 날 = 0.4 * 0.2 * 0.7 = 0.056

  • 구름 낀 날 - 비 온 날 - 해 뜬 날 = 0.4 * 0.4 * 0.3 = 0.048

  • 해 뜬 날 - 구름 낀 날 - 해 뜬 날 = 0.4 * 0.2 * 0.2 = 0.016

  • 해 뜬 날 - 해 뜬 날 - 해 뜬 날 = 0.4 * 0.7 * 0.7 = 0.196

  • 해 뜬 날 - 비 온 날 - 해 뜬 날 = 0.4 * 0.1 * 0.3 = 0.012

  • 비 온 날 - 구름 낀 날 - 해 뜬 날 = 0.2 * 0.4 * 0.2 = 0.016

  • 비 온 날 - 해 뜬 날 - 해 뜬 날 = 0.2 * 0.3 * 0.7 = 0.042

  • 비 온 날 - 비 온 날 - 해 뜬 날 = 0.2 * 0.3 * 0.3 = 0.018

어제 날씨의 관측값이 없는 상황에서 내일 날씨를 예측한 결과 내일 해가 뜰 확률은 43.6% 입니다.

지금까지 Sequential한 상태 중에서 어느 한 순간의 어느 관측값에 대해 확률을 구하는 문제를 해결해보았다면 어떤 관측값을 가질 확률이 높을까? 라는 문제도 해결 할 수 있습니다.

예를 들면 내일 어떤 날씨일까? 라는 문제를 해결할 수 있습니다. 모든 식을 적기에는 상당히 오래 걸리므로 간단히 말하면 이전의 공식을 전체 확률로 확대시킨 뒤 가장 높은 확률을 골라내면 끝납니다.

중요한 점은 HMM의 과정을 거쳐서 나온 값들은 덧셈을 사용한다는 점입니다. 따라서 곱셈 연산이 많아지면서 값이 0으로 수렴하는 에러가 발생하지 않으며 연산은 훨씬 가볍습니다.

HMM의 연산은 무척이나 많지만 Dynamic Programming 기법을 사용하여 연산을 최적화하는 방식을 채택함으로써 충분히 연산가능한 수준으로 사용할 수 있습니다.

제가 참고하며 공부 한 ratsgo님의 블로그에서 공식을 빌려와서 설명드리겠습니다.

\[\hat T = argmax_ {T}\ P(T|W)\] \[= argmax_ {T} \ P(W|T)\ ⋅ \ P(T)\] \[= argmax_ {T} \prod_ {i} {P(W_ {i} | T_ {i})} \prod_ {i} {P(T_ {i} | T_ {i-1})}\]

위에서부터

  1. 우리가 구하고 싶은 값은 Sequential한 데이터 W가 입력되었을 때 관측값 $\hat T$를 알고 싶습니다. 그러기 위해 우리는 가장 확률이 높은 T를 구하고자 합니다.

  2. Marcov 모델을 생각하면 이전의 관측값을 기반으로 $T$일 확률과 그 확률에서 $W$값의 확률을 구하는 공식으로 변환할 수 있죠. 이전의 관측값 $T$가 구하고자 하는 결과에 영향을 끼치니까요

  3. 그래서 이전의 T의 확률을 $T_ {i-1}$을 기반으로 $T_ {i}$의 확률을 구하는 공식과 $T_ {i}$를 기반으로 $W_ {i}$를 구하는 공식을 합치면 $\hat T$를 구할 수 있음을 알 수 있습니다.

3. Maximum Entropy Model

최대 엔트로피 모델은 간단히 말하면 Multinominal Logistic Regression (다중 로지스틱 회귀)라고 말할 수 있습니다. 이전의 정보를 사용하는 것은 단순 회귀기법으로도 구현 할 수 있습니다. Sequential한 성질을 사용하지 않을 수 있지만 이런 식으로 문제를 해결하면 이전의 관측값에 대해 가중치를 부여할 수 있습니다.

\[x_ {yesterday} = [sun, cloud, rain]\]

예측한 내일의 날씨를 \( \hat h \) 이라고 생각한다면 다음과 같은 선형회귀 식으로 나타낼 수 있습니다.

\[\hat h = x_ {yesterday} * w_ {1} + x_ {today} * w_ {2}\]

이 공식을 가지고 logistic function에 적용시키면 다음과 같은 [0,1] 사이의 공식으로 나타낼 수 있죠.

\[f(x_ {yesterday} , x_ {today}) = \frac {1} {1 + e^ {\hat h} }\] \[P(x_ {i}) = \frac{f(x_ {i-2}, x_ {i-1})} {\sum_ {i=1} ^ {n} {f({x_ {i-2}, x_ {i-1})}}}\]

식이 조금 바뀐 것 같지만 Sequential 데이터에서 $i = 내일의 날씨$ 로 가정하고 어제의 날씨와 오늘의 날씨를 i를 기반으로 나타냈을 때 위와 같은 식이 됩니다.

이전의 관측값을 기반으로 다음의 관측값을 예측하는 모델이라면 이렇듯 다중 로지스틱 회귀로도 가능합니다. 이러한 방식에서 장점은 엔지니어의 지식에 따라 다양한 파라미터를 추가할 수 있다는 점 입니다.

예를 들어 날씨와 관련된 우산의 판매량이나 기온의 변화량 등을 사용하면 더 유연한 모델을 만들 수 있을거라고 예상됩니다.

하지만 문제점으로는 Marcov Model처럼 Sequence 모델이 아니라는 점입니다. 이전의 정보를 가지고 예측하는 과정은 똑같지만 모델 자체가 Sequential Model은 아니죠. 단일 관측만이 가능한 모델입니다.

4. Maximum Entropy Marcov Model

이러한 이류로 MEMM이 등장하게 되었습니다. HMM과 같이 Sequential Model임을 유지하면서 동시에 MEM의 장점을 사용하기 위해서입니다.

\[\hat T = argmax_ {T}\ P(T|W)\] \[= argmax_ {T} \prod {P(T_ {i}|W_ {i},T_ {i-1})}\]

위의 식을 풀이하면 \($\hat T\)$ 상태는 \($W_ {i}\)$와 \($T_ {i-1}\)$ 일 경우의 \($T_ {i}\)$ 곱의 최대 값이다. 라고 말할 수 있습니다.

여기서 \( P(T_ {i} W_ {i},T_ {i-1}) \) 를 Maximum Entropy Model로 나타내면 됩니다.
\[P(T_ {i}|W_ {i},T_ {i-1}) = \frac{f(w_ {i}, T_ {i-1})} {\sum_ {i=1} ^ {n} {f({w_ {i}, T_ {i-1})}}}\]

이런 방식을 이용하면 엔지니어는 자신이 원하는 특징을 모델에 사용할 수 있으면서도 Sequential한 작업을 할 수 있습니다. $T_ {i-1}$을 구하는 작업에서도 동일한 작업을 사용하면 되기 때문이며, 그에 따른 파라미터는 학습을 통해 지속적으로 업데이트 할 수 있기 때문입니다.

이상으로 Sequential Model에 대한 공부를 마치겠습니다. 아직 많이 부족한 글로 혹시 틀린 점을 찾게 된다면 꾸준히 수정하겠습니다.

참고자료:

https://ratsgo.github.io/machine%20learning/2017/11/04/MEMMs/

https://untitledtblog.tistory.com/97

https://ratsgo.github.io/machine%20learning/2017/03/18/HMMs/