Gradient에 대해서

딥러닝에서 가중치를 학습하는 과정에서 필수적으로 사용하는 Gradient를 알아봅니다.

Layer를 통한 인공지능 학습을 진행하는 것은 추후 [포스팅]을 진행하겠습니다.

Gradient는 무엇인가?

사전적인 의미로 Gradient는 “기울기”입니다. 그러면 무엇의 기울기인지 알아봐야 할 것 같습니다.

딥러닝을 통해 우리가 알고 싶은 것은 실제 값의 분포를 표현하는 어떠한 규칙에 가능한 가깝게 예측 할 수 있는 모델입니다.

너무나 실제 학습 데이터에 가깝게 예측해버리면 우리는 Over Fitting이라고 하고 반대로 너무 실제 학습 데이터에 멀리 예측해버리면 우리는 Under Fitting이라고 하죠.

즉, Fitting을 통해 우리는 실제 분포에 가깝게 표현하고 과하지도 부족하지도 않게 학습을 진행합니다.

Gradient는 이 Fitting을 하는 과정에서 사용되는 기울기입니다.

\[\hat{Y} = xW + b\]

위의 Hyperthesis를 연산하는 과정에서 우리는 $W$와 $b$를 바꾸어 $\hat{Y}$를 실제 값의 분포인 $Y$에 가깝도록 만들어야 합니다.

우리는 실제 값에서 Hyperthesis를 통해 얻어진 값의 차이를 Loss라고 표현하며 우리가 얼마나 잘못 예측했는지를 알 수 있습니다.

\[Loss_{MSE} = \sum(Y - (xW+b))^2\]

그러면 $W$와 $b$를 최적화하는 것이 무엇을 말하는 걸까요? $W$값이 작아지거나 커지거나 혹은 $b$값이 커지거나 작아지거나 와 같은 변화가 발생하는 것이 최적화하는 방법입니다. 그래야 $\hat{Y}$의 값이 바뀌고 $Loss$가 줄어드니까요.

그럼 이렇게 말할 수 있습니다.

“$Loss$가 줄어드는 방향으로 $W$와 $b$가 이동하는구나”

그러면 의문이 구체화됩니다.

“$Loss$가 줄어드는 방향은 어떤 방향일까?”

이 의문을 해결하기 위해 Gradient가 존재합니다. 우리는 다음의 과정을 통해 예측을 한다고 생각해보겠습니다.

\[\hat{Y} = xW + b\]

위의 식이 주어질 때 이러한 질문을 받으면 어떻게 대답할 수 있을까요? “$x$가 1커질 때 **$\hat{Y}$ 은 어떻게 변하나요?”** 답은 “$W$만큼 커집니다.”입니다.

이 사실을 우리는 편미분을 통해 알 수 있죠. $\hat{Y}$를 $x$로 편미분을 하면 우리가 알고싶은 x가 1증가 할 때 \hat{Y}에 미치는 영향을 알 수 있습니다.

이러한 방식을 Backpropergation이라고 합니다.

이걸 그대로 적용해서 Layer에 적용해봅시다.

FC Layer(1) -> Sigmoid Layer -> FC Layer(2) -> Sigmoid Layer -> FC Layer(3) -> $Loss_{Y-Output}$

Loss에서 역방향으로 편미분을 통해서 각 파라미터가 얼마나 영향을 가지고 있는지 알아봅니다. $Loss$를 $W_3$으로 편미분하면 $W_3$이 $Loss$에 얼마나 영향을 미치는지 알 수 있겠네요. 마찬가지로 $x_3$을 $W_2$로 편미분하면 $x_3$에 $W_2$가 얼마나 영향을 미치는지 알 수 있습니다. 물론 Sigmoid를 통과 한 후의 결과에 대한 값이지만, 설명에서는 활성화함수 연산을 무시하겠습니다.

그리고 그 값을 식으로 적으면 다음과 같습니다.

\[\frac{\partial{Loss}}{\partial{W_1}} = \frac{\partial{Loss}}{\partial{W_3}} \frac{\partial{W_3}}{\partial{W_2}} \frac{\partial{W_2}}{\partial{W_1}}\]

여기서 $\frac{\partial{Loss}}{\partial{x_1}}$ 가 의미하는 바가 $W_1$이 Loss에 미치는 영향 이라는 점을 알면 연산이 얼마나 간소화 되는지 알 수 있습니다. 이러한 방식을 Chain Rule을 통한 Gradient 계산이라고 말합니다.

우리는 이제 $W_i$ 가 $Loss$에 미치는 영향을 알 수 있는 무기가 생겼습니다. 상세하게 말하면 $W$가 양 또는 음의 영향을 미치는지 추가적으로 얼마나 크게 영향을 미치는지 알 수 있습니다.

이제 $Loss$를 줄이고 싶다면 $W$를 음의 방향으로 움직이게 하고 반대라면 양의 방향으로 움직이게 하면 됩니다.

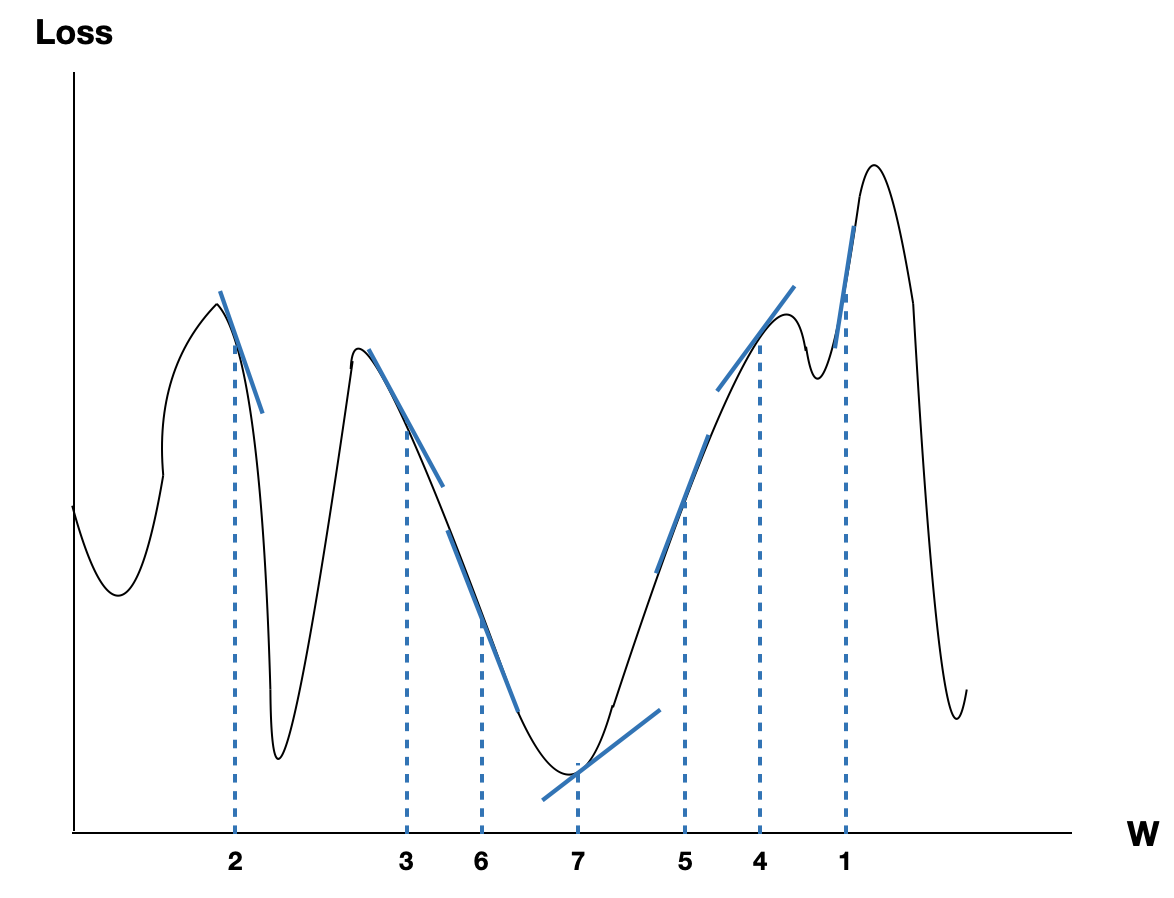
해당 미분값이 양수라면 $W$를 크게 하면 $Loss$가 커지고 반대로 작게하면 $Loss$가 작아지는 걸 알 수 있습니다. 만약 음수라면 $W$를 크게 하면 $Loss$가 작아지고 반대로 작게하면 $Loss$는 작아집니다. 이해하기 쉬운 그래프를 하나 더 올리겠습니다.

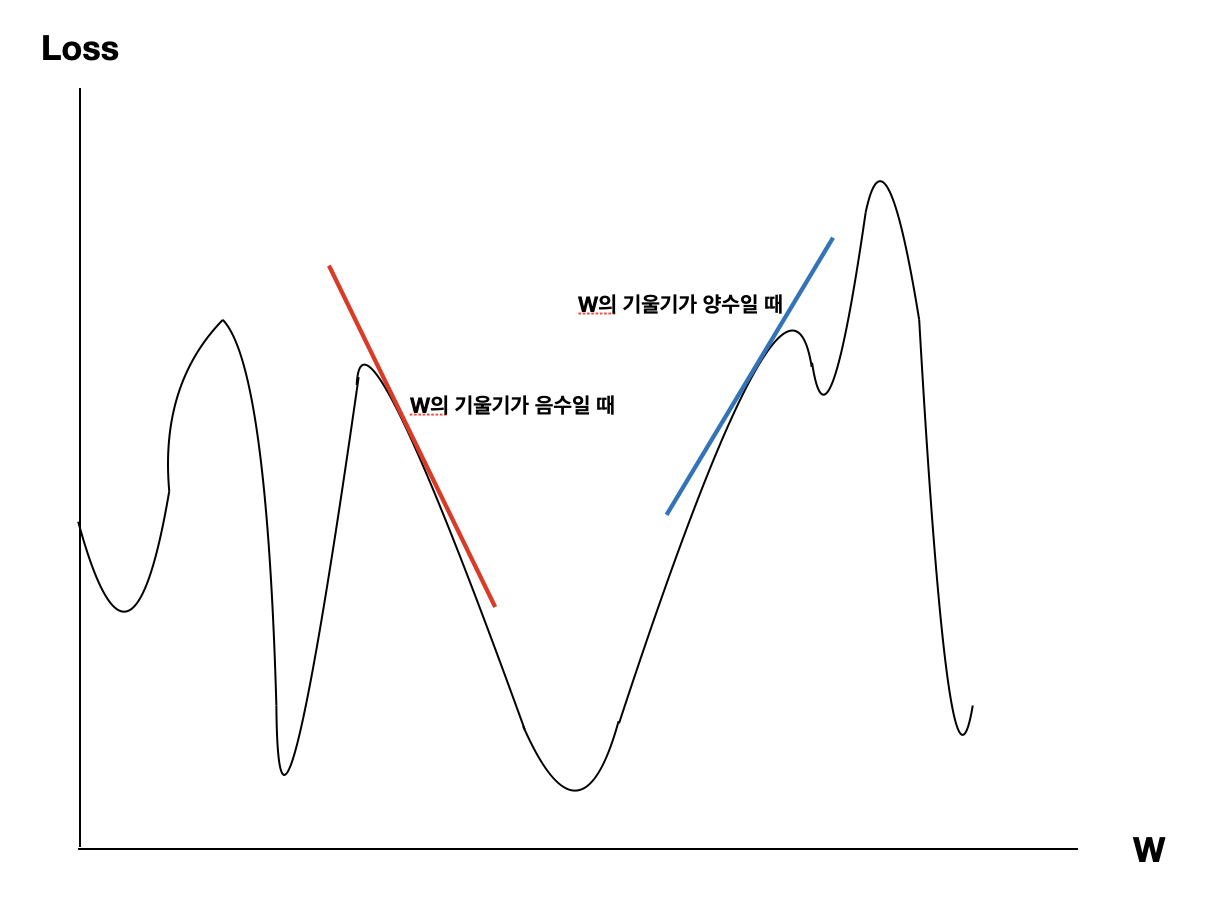
Y축은 Loss이고, X축은 W라고 생각하시면 됩니다.

이제 Gradient가 무엇인지 알 수 있습니다. 위의 그림에서 우리는 경사를 따라 내려가는 학습을 진행합니다. 그리고 그 경사가 Gradient 입니다. 그리고 이러한 학습 방식이 Gradient Descent 입니다.

그러면 Gradient Descent는 어떻게 진행할까?

Gradient Descent는 $W$의 순간변화율을 구하고 $Loss$가 최소가 될 수 있는 방향으로 이동하는 방법입니다.

계속해서 $Loss$가 최소가 되는 방향으로 학습을 하다보면 기울기는 점점 0에 가까워집니다. 그러다보면 점점 학습은 수렴하게 되는 것입니다.

여기까지만 계산하면 다음의 식이 나오겠네요.

$W = W - \frac{\partial{Loss}}{\partial{W}}$

그런데 이렇게 학습을 진행해버리면 문제가 생깁니다. 한 번의 학습으로 $W$가 너무 크게 학습되어버리면 기울기가 0으로 수렴하지 않을 수 있습니다. 혹은 아예 튕겨져 나갈수도? 있겠네요.

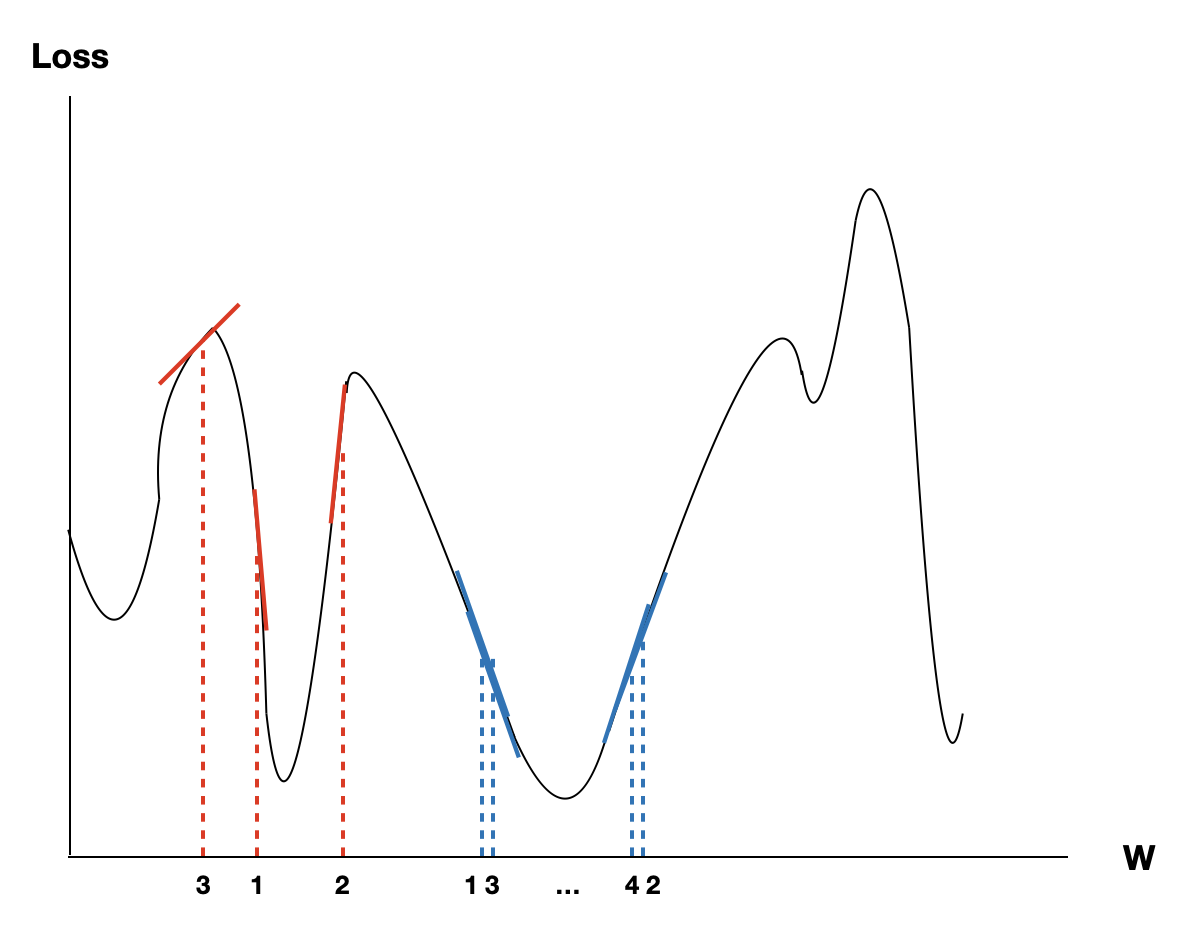
여기서 Learning Rate가 등장합니다.

$W = W - lr\frac{\partial{Loss}}{\partial{x}}$

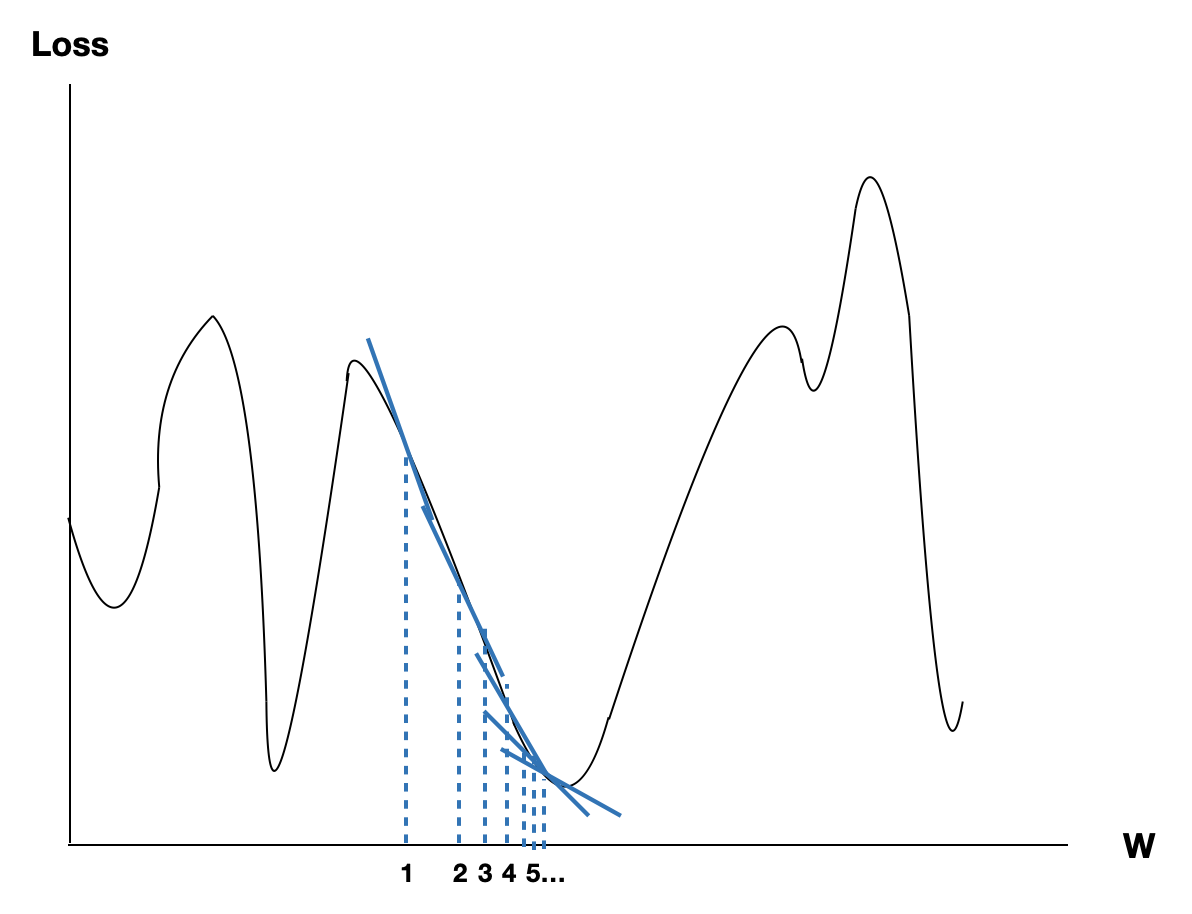
Learning Rate가 있으니 학습은 천천히 진행됩니다. 예를들면 Learning Rate가 0.01이라면 다음의 식이 되겠네요.

$W = W - 0.01\frac{\partial{Loss}}{\partial{x}}$

학습의 진행도 다음처럼 천천히 진행되게 됩니다.

Gradient Descent의 문제점은 무엇일까?

지역 최소점

Gradient를 따라 하강하는 과정을 거치면 우리는 항상 최소의 Loss를 알 수 있을까요? 사실은 그렇지 않습니다.

현재 하강하고 있는 Gradient가 최소 $Loss$를 얻을 수 있는 Gradient가 아닐 수 있거든요. 예를 들면 다음의 그래프로 알아보겠습니다.

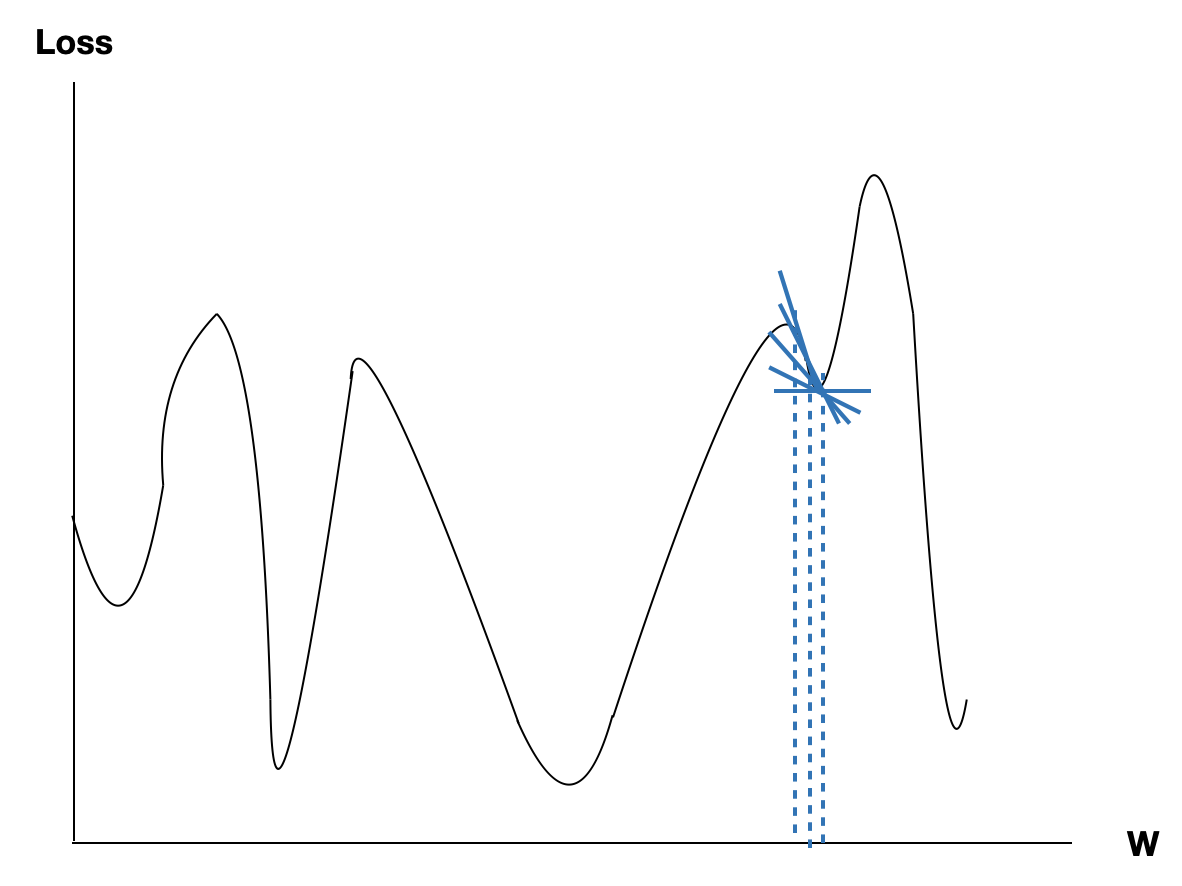
위의 그래프는 Gradient가 0으로 수렴해가지만 최소 Loss와는 거리가 멀어보입니다. 이렇듯 최소 $Loss$가 아니지만 경사를 따라 학습되어지는 최소지점을 지역 최소점이라고 합니다.

이 문제는 Learning Rate를 잘 조절하면 어느정도의 해결은 되지만 완전한 해결방식은 아니고 언제까지나 “기대사항” 정도 밖에 되지 않기 때문에 이 문제를 해결할 수 있는 방법을 제안하게 됩니다.

다양한 Gradient Descent 방식

SGD

SGD는 Stochastic Gradient Descent의 약자입니다. Stochastic은 “확률적”이라는 의미입니다. 어딘가 믿음직스럽지 않은 이름이네요. 대체 어디가 확률적이라는걸까요?

기존의 GD는 전체 데이터를 기반으로 학습을 진행했습니다. 위에서 본 것처럼 GD의 문제점이 발생합니다. 그러한 문제점을 극복하기 위해서 SGD가 개발되었습니다.

전체 데이터가 포함한 부분집합을 학습하면 대체적으로 최소 $Loss$를 얻을 경사 주변에서 학습되지 않을까? 정도의 개념으로 발전하게 된 학습이 아닐까 생각됩니다.

저는 데이터를 경향으로 말합니다. 그리고 예측은 경향을 알아보는 것으로 말합니다.

모든 데이터가 어떠한 큰 경향을 띄고 있다면 대체적으로 부분집합 또한 그 경향을 띌 것이고, 학습이 진행되면서 그 경향성이 조금씩 진해 질 것이라고 가정합니다.

굳이 그림을 그리자면 다음과 같지만, 사실 학습에 사용되는 데이터 셋이 바뀌기 때문에 분포또한 달라지게 되고 그래프도 달라지게 되서 다음의 그림과는 조금 다릅니다만 대체적으로 좋은 결과로 이동합니다.

일반적인 Gradient Descent와 비교하면 다음과 같은 그림이 나온다고 합니다.

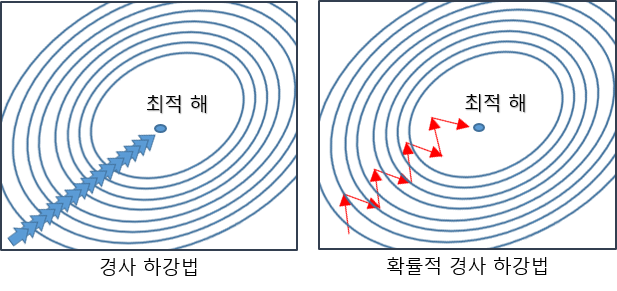
SGD는 Batch Size만큼의 데이터 셋을 임의로 분할해서 학습하는 방식으로 처음에는 Gradient가 통통 튀기 시작하지만 점차 수렴해나가는 모습을 보여줍니다.

기존의 GD보다는 연산이 많이 수행되기 때문에 학습 시간이 오래 걸리는 문제도 있습니다만, 지역 최소점을 피할 확률이 높습니다.

이 후의 방법론은 모두 SGD를 기본으로 사용하며 Learning Rate 계산을 조금 수정하여 더욱 좋은 성능을 얻고자 하는 알고리즘들입니다.

Momentum

조금 더 발전시킨 방법으로 Momentum을 사용 할 수 있습니다.

지역 최소점에 왜 걸리게 될까? 를 고민하던 사람들은 곧 Gradient만으로 이동 거리를 계산하기에는 한계가 있다는 생각을 하게 됩니다. 그래서 가던 방향으로 조금 더 이동시켜보면 어떨까?라는 생각을 하게 됩니다. Gradient와 Learning Rate외에 이동 할 수 있는 파라미터를 하나 추가하게되죠.

바로 관성계수 $m$입니다.

\[V_t​=m×V_{t−1}​−\eta\nabla_ω​J(ω_t​)\] \[ω_{t+1}​=ω_t​+V_t​\]

간단히 설명하면 처음 학습은 $V_{t}$는 0이기 때문에 GD와 똑같이 기울기와 Learning Rate의 곱 만큼 학습됩니다. 그 이후 $m$과 $V$의 곱에서 학습 계수만큼 뺀 값만큼 학습이 진행되면서 우리가 말하는 경사를 빠르게 내려오게 됩니다. 즉 수렴속도가 빨라지며, 지역 최소점이 낮은 경사를 이루고 있다면 그 언덕을 넘어 갈 수도 있습니다.

이렇게 하면 지역 최소점을 넘어 갈 수도 있고, 경사가 0에 가까운 상황에서도 학습이 진행되어 평평한 Gradient에 걸릴 경우도 넘어 갈 수 있습니다.

Adagrad

또 다른 방법으로 가중치마다 움직이는 정도를 조절해버리자는 생각에도 도달하게 됩니다.

이미 많은 학습이 진행 된 가중치는 작게 학습하여 수렴하도록하고 적게 학습 된 가중치는 크게 학습하여 지역 최소점을 벗어나 좋은 Gradient를 찾자 라고 말해보겠습니다.

\[G_t​=G_{t−1}​+(\nabla_ω​J(ω_t​))^2=\sum_{i=1}^k​\nabla_{ω_i}​​J(ω_i​)\] \[ω_{t+1}​=ω_t​−\frac{\eta}{\sqrt{G_t}​+ϵ}​⋅\nabla_ω​J(ω_t​)\]

위 식에서 $G_t$는 이전 이동까지 사용했던 기울기 값($G_{t-1}$)의 제곱의 합에서 현재 기울기 값의 제곱을 더해줍니다. 결국 현재까지 이동했던 거리를 말합니다.

그리고 현재까지 이동했던 거리가 커질수록 Learning Rate는 점점 작아지기 때문에 학습은 조금씩 진행됩니다.

처음 이동 거리는 0이기 때문에 zero division 문제를 방지하기 위해서 $\epsilon$을 매우 작은 수로 설정하여 사용합니다.

이러한 방식에 문제가 아예 없는 것은 아닙니다. 학습이 진행 될 수록 $G_t$는 커지게 되고 Learning Rate가 0으로 수렴하게 되면서 점차 아예 학습이 진행되지 않을 수 있습니다.

그렇게 RMSProp이 등장하게 되었습니다.

RMSProp

RMSProp은 Adagrad에서 이동 거리를 계산하는 과정을 조절합니다.

\[0 \leq \gamma \leq 1\] \[G_t​=\gamma G_{t−1}​+(1-\gamma)(\nabla_ω​J(ω_t​))^2\] \[ω_{t+1}​=ω_t​−\frac{\eta}{\sqrt{G_t}​+ϵ}​⋅\nabla_ω​J(ω_t​)\]

$G_t$를 계산하는 과정만이 바뀐 사실을 알 수 있습니다. 일반적으로 $\gamma$ 는 0.9이상의 값이 주로 사용되며, 이동거리 자체를 스케일링하여 학습이 0으로 수렴하는 것을 어느정도 방지 할 수 있습니다.

Learning Rate가 0으로 수렴할 정도로 $G_t$가 커지면 1보다 작은 값으로 곱하면서 일정 수준 이상으로 커지는 것을 방지합니다. 심지어 이동거리를 더하는 과정에서도 1보다 작은 값이 곱해지며 $G_t$의 커짐을 방지합니다.

Adam

여기에 Momentum을 추가하면 어떨까요?

총 이동거리에 반비례해서 천천히 움직이면서 Gradient가 0에 가까워도 학습을 더 진행 할 수 있는 방식이 Adam입니다.

\[m_t​=\beta_1​m_{t−1}​+(1−\beta_1​)\nabla_ω​J(ω_t​)\] \[V_t​=\beta_2​m_{t−1}​+(1−\beta_2​)(\nabla_ω​J(ω_t​))^2\] \[ω_{t+1}​=ω_t​−m_t\frac{\eta}{​V_t​+\epsilon}​\]

처음으로 설명 할 것은 단연 관성계수인 $m$입니다. Momentum에서 사용했던 방식과 마찬가지로 기울기 값을 일정 수준 더해주는 과정을 거침으로써 같은 방향으로 학습 할 때 커지는 관성을 표현해줍니다.

그 후 관성계수를 현재 이동 거리로 가정하고 RMSProp을 적용해줍니다. 기존의 기울기를 관성계수로 치환하고 Learning Rate를 $V_t$를 이용하여 반비례하게 정의해주면 다음 가중치는 관성의 성질을 가지지만 학습이 진행되면서 점차 이동거리가 줄어드는 바람직한(?) 학습이 진행됩니다.

참고

https://twinw.tistory.com/247 https://onevision.tistory.com/entry/Optimizer-의-종류와-특성-Momentum-RMSProp-Adam