Document Clustering ( 문서 군집화 )
문서 군집화는 비슷한 문서들을 하나의 군집으로 묶는 것을 목표로 합니다. 즉 동일한 군집에 속한 데이터는 비슷한 문서임을 가정하는 방법입니다. 결과적으로 텍스트 데이터의 특징 상 동일한 군집에 속한 데이터는 같은 주제에 대한 이야기를 할 가능성이 높게 됩니다.
문서를 군집화하기 위해서는 문서들이 얼마나 차이가 나는지, 혹은 얼마나 유사한지를 알아야 합니다. 즉 문서가 수치적인 데이터로 변환되어야 하며, 두 데이터의 차이가 계산되어야 합니다.
예를 들면, 다음과 같은 3개의 문장이 있다고 생각해보겠습니다.
A = “나는 고양이가 좋아”
B = “나는 강아지가 좋아”
C = “저기 지나가는 고양이가 나를 바라본다.”
이 예제를 군집해보았을때 A와 B가 하나의 군집에 속해있다면 내가 좋아하는 것에 대해 유사한 데이터 의 개념으로 군집이 된 것이고, A와 C가 하나의 군집이 되었다면 고양이에 대해 유사한 데이터 개체의 개념으로 군집이 된 것으로 볼 수 있습니다. 하지만 두 개의 케이스 모두 어느정도 유사한 개념의 군집이 만들어 짐을 알 수 있습니다. 그리고 우리가 알 수 있는 점은 어떤 개념으로 군집이 생성되었는지 알 수 없다. 정확히는 컨트롤 할 수 없다. 는 점입니다. 이 점은 군집화의 중요한 특징입니다.
또 다른 큰 특징은 바로 비지도 학습 으로 작동한다는 점입니다. 비지도 학습이란 각 데이터에 대한 답이 주어지지 않아도 작동하는 머신러닝 방식입니다. 답을 제공하지 않아도 되는 작업들 비슷한 것을 묶거나 표현 방식을 바꾸는 등에 자주 사용되는 방식입니다.
그러면 군집화의 특징을 살펴보았으니 어떻게 군집이 형성되는지 공부해보겠습니다.
Distance Or similarity
문서들이 서로 가까운지 혹은 멀리 있는지를 이해하려먼 distance 혹은 similarity에 대한 개념을 이해 할 필요가 있습니다. 쉽게 설명하면 distance는 얼마나 멀리 있는지에 대한 정도이며 similarity는 얼마나 가까이에 있는지에 대한 정도 라고 생각할 수 있습니다. 그림으로 표현하면 다음과 같습니다.
몇몇 공식은 두 가지 표현방식 중 어느 것이든 사용 할 수 있습니다. 사실 변수의 range가 정해져있다면 distance를 similarity로 변환 할 수 있고 그 반대도 얼마든지 성립되기 때문입니다. 하지만 일반적으로는 distance를 사용합니다. 이유는 이어지는 내용에서도 설명드리겠지만, 변환 할 수 없는 euclidean distance와 entropy를 사용한 거리 공식을 사용한 방식도 있기 때문에 일정한 scale이 없어 similarity로 표현할 수 없기 때문입니다.
그럼 distance의 종류를 살펴보겠습니다.
1. euclidean distance
euclidean distance는 머신러닝을 공부하면 흔하게 볼 수 있는 거리 공식입니다. l2 distance 라고도 불리며 피타고라스 정리와 유사하게 두 위치 사이의 거리를 구하는 공식이라고 생각하면 됩니다.
\[\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2...}\]가장 일반적인 만큼 강력한 성능을 가졌지만 고차원의 데이터일 경우 문제가 생길 수 있습니다. 그 문제점은 바로 데이터의 차원이 클수록 유클리디안 거리는 작은 차이에도 큰 거리를 갖게 되는 점입니다. 주로 군집화 방식을 사용할 때 TF-IDF 표현방식을 통한 SparseMatrix를 사용하는데 대부분의 데이터의 값이 0이며 비교 데이터가 해당 값을 가지고 있을 경우 오차는 크게 계산됩니다.
때문에 정말 유사한 데이터가 아닌 경우 너무나도 먼 거리를 갖게 되어버리는 결과가 생깁니다. 각 단어의 수 만큼 차원을 갖는 텍스트 데이터의 경우 euclidean distance는 조심히 사용해야 합니다.
2.cosine distance
cosine distance는 cosine similarity를 이용하여 구하는 거리입니다.
cosine similarity는 euclidean distance와는 다르게 두 위치 사이의 각도로 계산되는 방식입니다. 공간상에서 유사한 방향으로 뻗은 벡터라면 유사한 데이터라는 가정으로 만들어진 방식이며, 실제로도 텍스트 분석에서 자주 사용되는 거리공식입니다.
cosine similarity는 다차원의 공간에서 유용하게 사용할 수 있는데 일단 cosine의 범위는 [-1,1] 사이로 고정되어 있으며 텍스트 데이터의 표현방식 중 Bag Of Words는 음수를 갖지 않기 때문에 범위를 [0,1]로 확정지을 수 있기 때문입니다. 일치하는 데이터가 없다면 0, 완벽히 일치하면 1의 값을 갖는 비교방식은 유사한 정도를 알기에 좋은 방식입니다.
\[{\displaystyle \mathbf {a} \cdot \mathbf {b} =\left|\left|\mathbf {a} \right|\right|\left|\left|\mathbf {b} \right|\right|\cos \theta }\] \[\cos \theta = \frac{a \cdot b}{\left|\left|\mathbf{a}\right|\right| \left|\left|\mathbf{b}\right|\right|}\] \[-1 < cos(\theta) < 1\] \[if(a_i >= 0, b_i >= 0): 0 < cos(\theta)<1\]하지만 이 값은 similarity이기 때문에 distance를 구하기 위해서는 최대 값인 1에서 cosine similarity를 빼면 됩니다.
\[dist(a,b) = 1-cos(\theta)\]3.jaccard distance
jaccard distance는 집합의 개념으로 알아볼 수 있는 두 데이터 사이의 거리 공식입니다. 그렇기 때문에 카테고리 형식으로 구분되어 있는 데이터에 사용 할 수 있으며, 우리가 사용하는 텍스트 분석에 사용할 수 있는 방식이라고 생각할 수 있습니다.
jaccard similarity의 공식은 다음과 같습니다.
\[J_{sim}(A,B) = {|A \cap B| \over{|A \cup B|}}\] \[0 <= J_{sim} <= 1\]단어 단위의 텍스트 분석에서 위의 jaccard similarity가 말하는 것은 두 문장에서 사용된 총 단어 중에서 동시에 사용된 단어 의 정도입니다. 이 점수를 가지고 우리가 얻고자 하는 distance를 얻으려면 1을 빼주면 됩니다. 왜냐하면 similarity의 값이 [0,1]이기 때문이죠.
\[J*{dist} = {1 - J*{sim}}\]4.Pearson correlation coefficient
흔히 상관계수라고 알고 있는 통계적 방법 중 가장 널리 쓰이는 방식입니다. 일반적으로 상관관계라는 말은 이 Pearson correlation coefficient입니다. 그러므로 짧게 상관관계라고 말하겠습니다.
상관관계는 공분산에서 표준편차의 곱을 나눈 값이라고 말합니다. 저도 수식에 약한 편이므로 최대한 간단한 수식으로 설명 드리겠습니다.
\[Cov(X,Y) = {\sum^N(X-\mu_X)(Y-\mu_Y)\over{N}}\] \[Pearson_{corr} = {Cov(X,Y)\over{\alpha_X \alpha_Y}}\] \[N = 집단\ 내\ 개체수\]먼저 공분산을 구하는 공식을 보면 두 확률분포의 각 편차의 곱을 N번 수행하여 결과를 N으로 나누어줍니다. 즉 두 값의 편차의 평균이 유지된 상태가 되며 공분산은 두 확률분포 상에서 양의 관계, 혹은 음의 관계를 가졌는만을 알려주기 때문에 이를 두 데이터의 표준 편차의 곱으로 나누어주면 [-1, 1]의 값을 가진 상관계수가 나오게 됩니다.
공분산의 문제인 두 확률분포가 얼마나 상관성이 있는지 를 알 수 있게 되어 비교할 수 있는 지표로 사용할 수 있습니다.
5.Averaged Kullback-Leibler Divergence
Kullback-Leibler Divergence는 기본적으로 similarity와 distance 개념으로 만들어진 개념은 아닙니다. 정확히는 두 확률분포를 차이를 알기 위해 사용하는 방식입니다. 예를 들면 P의 분포에 비해 Q의 분포는 얼마나 차이가 나는가? 를 알기위한 방식입니다.
중요한 점은 entropy를 이용하기 때문에 이전의 방식과는 달리 스케일이 정해져있지 않습니다. 또한 기준으로 잡은 분포에 따라서 값이 달라집니다. 분포 X를 기준으로 분포 Y와의 차이에 대한 entropy와 분포 Y를 기준으로 분포 X와의 차이에 대한 entropy는 그 기준이 달라집니다.
일정한 스케일이 정해지지 않더라도 우리는 군집화를 할 수 있습니다. 제가 알고싶은 것은 1을 기준으로 얼마나 거리가 떨어져있는지, 가 아니라 두 데이터가 얼마나 차이가 나는가, 얼마나 멀리 떨어져있는가, 이기 때문에 차이를 정의할 수 있다면 스케일이 정해져있지 않아도 충분합니다.
그런 이유로 Anna Huang - similarity Measures for Text Document Clustering 논문에서 이 방식을 사용할 것으로 생각합니다.
\[D_{KL}(P|Q)=\sum_iP(i)\log {\frac {P(i)}{Q(i)}}\]확률분포 P를 기준으로 분포를 Q로 대체했을 때 얼마나 정보량의 차이가 있는가 에 대한 공식입니다. 여기서 2가지의 문제가 생깁니다.
$D_ {KL}(P\text{\textbar}Q)$과 $D_ {KL}(Q\text{\textbar}P))$ 두 값은 다르지만 우리는 두 분포의 차이를 명확한 값을 구해야합니다.
$D_ {KL}(P\text{\textbar}Q)$ 의 공식 중 $log(P(i))\over{log(Q(i))}$ 에서 $log(Q(i))$ 가 0의 값을 가지면 inf(무한대)의 값을 가집니다. 즉 BagOfWords에서 해당 단어가 없을 경우, 분모가 0이 되며, 해당 분포의 차이는 무한대로 확정됩니다.
여기서 제가 선택한 방법은 다음과 같습니다.
\[{D_ {KL}(P|Q)} + {D_ {KL}(Q|P)} \over{2}\]완벽한 방법이라고 볼 수는 없지만 두 값이 모두 P와 Q의 분포 차이를 말한다면 평균을 내는 방법을 사용했습니다. 사실 제대로 사용하려면 entropy의 스케일에 대한 고려도 충분히 포함되어야 하지만, 아직 부족한 수학적 지식이므로…
\[min(P(i)) = 1-e5\]각 요소의 최소값을 지정하는 방식을 사용하여 log연산의 무한대로 발산하는 문제를 해결했습니다.
K-means Clustering
돌고 돌아서 K-means Clustering을 시작하게 되었습니다. K-means 알고리즘을 순차적인 진행방법을 말씀드리면 다음과 같습니다.
- k개의 Representation Point를 임의의 요소의 벡터로 선택한다.
- 전체 데이터에 대해 Representation Point와의 거리를 계산한다.
- 해당 데이터의 군집을 가장 가까운 거리에 있는 Representation Point와 같은 군집으로 할당한다.
- 각 군집의 Representation Point를 해당 군집을 가진 데이터의 평균으로 업데이트한다.
- 전체 데이터를 기반으로 2-4단계를 다시 진행한다.
과정에서 알 수 있듯이 데이터를 가장 잘 군집화 하는 Representation Point를 찾아가는 과정이 바로 K-means 군집화입니다. 제대로 위치를 찾아내면 각자 자신의 주변 데이터에 대해 군집화하기만 하면 각 군집에 속한 데이터를 찾을 수 있는 것이죠.
쉬워보이지만 제가 만든 Clustering은 엄청난 시간이 소모됩니다. 나름대로 최적화를 하고 싶었는데, 추후에 k-means를 뜯어봐서 수정하도록 하겠습니다.
첫번째로 initialize입니다. k-means에서는 초기 Representation Point를 설정하는 것이 매우 중요합니다. 어느 한 벡터로 수렴하게 될 Representation Point가 서로 붙어있게 되면 제자리를 찾아가는 동안 많은 반복횟수를 가지게 되고, 그만큼 k-means는 느려지게 됩니다.
그래서 최적의 초기값은 Representation Point가 가능한 멀리 분포되어있는 형태입니다. 그렇게만 되면 각 군집은 반복을 거쳐가면서 최적의 Point로 빠르게 찾아 갈 수 있게 됩니다.
k-means initialize
random initialize
적힌 그대로 랜덤으로 초기화를 시키는 방법입니다. 현재 이 방법으로 알고리즘을 만들었으며, 덕분에 엄청난 시간이 소요되는 것을 알 수 있습니다. 운이 좋게 서로 멀리 떨어져있는 요소들을 잡는다면 좋은 성능을 보이겠지만, 그렇지 않으면 최악의 성능을 보일 수 있습니다.
random initialize - Maximum entropy score
k-means++ 와 Ball cut 방법을 사용하기 전 random initialize로 최대한 좋은 대표벡터를 얻기 위해서 고안한 방법입니다. 제가 임의로 만든 방법이라 좋은 성능이 나올지는 조금 더 공부를 해 봐야겠지만 좋은 대표 벡터의 조건이 균등하게 데이터를 구분하는 벡터라는 가정이라면 그 지점은 entropy가 높은 지점일 것이라는 예측에서 생각한 방법입니다.
entropy는 데이터의 크기에 따라 값이 달라지므로 군집을 시작하는 순간 최대 엔트로피는 정해지므로 그 값으로 현재 엔트로피를 나누면 score 형태 [0,1]를 구할 수 있을 것이라 생각하고 구현해보았습니다.
다만 이 방법은 여러번의 initialize 과정이 동반하므로 k-means++에서는 사용 할 수 없을 것으로 보입니다. 너무 오래걸릴 것 같거든요…
k-means++
k-means++는 거리를 기반으로 다음 초기값의 확률분포를 만드는 방법입니다. 하지만 이 방식은 텍스트 데이터에서 큰 성능을 보이지 않음을 lovit님의 블로그(링크)에서 알 수 있습니다. 이유는 backOfWords의 특성상 가까운 거리는 큰 의미를 가지지만 먼 거리에 대해 의미를 논하기에는 sparseMatrix의 데이터는 대체적으로 먼 거리로 측정이 되기 때문입니다.
즉 단어 1개가 1개의 차원을 나타내는 고차원의 데이터 셋에서는 k-means++에서 원하는 거리 기반 확률분포는 큰 효과를 갖지 못한다는 것입니다.
Ball cut
Ball cut은 그러한 고차원상의 k-means++를 대체할 방법으로 설명되어 있었습니다. 파라미터 \($t\)$를 설정하고 한 점을 선택할 때 거리가 \($t\)$ 이하인 점을 전부 삭제하는 방식으로 진행됩니다. 그렇게 벡터 공간이 비거나 혹은 k개의 군집을 만들게 되면 초기화를 끝내고 혹시나 벡터 공간이 k개의 군집을 선택하기 전에 비어버린다면 선택되지 않은 모든 점들 중 랜덤으로 초기화를 하는 방식입니다.
k-means clustering fitting
본격적으로 k-means를 실행시켜보겠습니다. 기준은 random sampling initializer으로 초기화를 시킨 뒤 단계를 밟아가며 진행하는 과정입니다.
첫 번째로 initialize를 진행합니다.
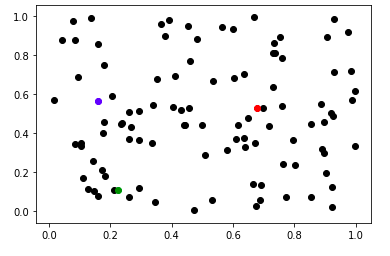
위의 그림에서 검은 점으로 표시된 데이터 중 파랑, 빨강, 초록색으로 표시 된 점이 바로 Random initialize한 점입니다. 그리고 해당 점을 통해 가장 가까운 데이터를 표시하면 이 부분이 첫번째 과정인 k개의 Representation Point를 정하는 곳이고, 다음 단계로 이 점들과 가장 가까운 데이터들을 표시하면 다음과 같은 그림이 나옵니다.
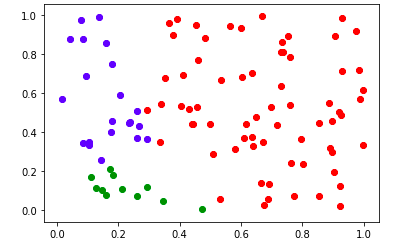
빨간색이 가장 큰 면적을 차지고하고 있군요, 2차원 공간으로 확인하니 initialize의 중요성을 확실하게 알 수 있습니다. 그리고 같은 군집에 있는 데이터들의 평균으로 Representation Point를 바꿔가며 2-4번 까지의 과정을 3번 거치면 Representation Point는 다음과 같이 바뀝니다.
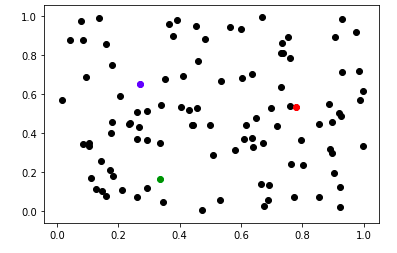
첫 initialize와 비교하면 파란점과 초록점은 점차 가운데로 모여드는 느낌으로 이동하고, 빨간색은 조금 중앙에서 멀어집니다.
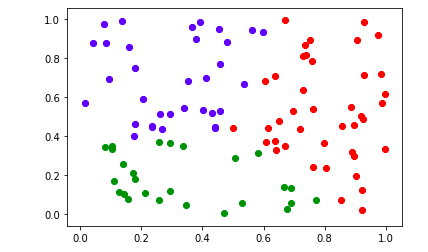
처음 그림보다 데이터들은 어느정도 편파적인 성향이 사라짐을 볼 수 있습니다. 그리고 이러한 변화는 어느정도의 반복에서 수렴하게 됩니다. 즉 더 이상 Representation Point의 변화가 없어지며 벡터는 수렴하여 움직이지 않게 됩니다. 그때, K-means는 멈추게 됩니다. 비록 Representation이 완벽하게 수렴하지 않더라도 K-means 알고리즘에서는 max_iter라는 파라미터를 이용하여 몇 번 반복할 것인지 정할 수 있습니다.
이로써 K-means Clustering 공부를 마치겠습니다.
reference
-
https://m.blog.naver.com/istech7/50153288534
-
https://lovit.github.io/nlp/machine%20learning/2018/10/16/spherical_kmeans/
-
Anna Huang. Similarity measures for text document clustering. In Proceedings of the sixth new zealand computer science research 20 student conference (NZCSRSC2008), Christchurch, New Zealand, pages 49–56, 2008