편향과 분산에 대해서
인공지능 분야에서 편향이라는 단어에 이해한다고 생각했지만, 정확히 설명하기 어려운 부분이라 생각되어 정리합니다.
편향 ( Bias )
편향은 데이터 분석을 하다보면 자주 듣게 되는 것 같습니다.
1. 선형회귀 식 에서의 편향 (b)
\[Hyperthesis = xw + b\]대체 선형회귀의 Hyperthesis에서 왜 b를 더해주는 걸까요?
많은 사람들이 이야기합니다. “활성화 함수를 평행이동 시킬 수 있잖아요!” 그리고 또 많은 사람들이 대답합니다. “그게 무슨 말이에요?!”
오늘은 이 부분을 명확하게 설명드리겠습니다.
왜? 우리는 분산을 사용하는지, 그리고 왜 활성화 함수를 평행이동 시키는 지 알아보겠습니다.
다음의 문제를 한 번 풀어보겠습니다.
Lion2me가 공부한 시간에 비해 얻은 시험 점수가 있습니다. 다음 시험에서 K시간 공부했을 때 얻을 수 있는 시험 점수를 예측해주세요.
그리고 회귀 식을 이용한 하나의 레이어를 거친 값이 $X_2$ = [8.4, 7.7, 8.1] 라고 가정해보겠습니다.
편향을 사용하지 않고 순수하게 $Y = xw$ 공식만을 사용했다고 가정합니다.
\[NextLayerinput = Sigmoid(wx)\]다음 레이어에 전달되는 input은 위와 같습니다.
그럼 $Sigmoid(X_2)$는 얼마일까요?
$Sigmoid(X_2)$ = [0.9997,0.9995,0.9998] 입니다. Sigmoid의 특성 상 숫자가 커지면 1에 수렴하고 작으면 0으로 수렴합니다. 그리고 수렴 할 수록 기울기는 점차 줄어들며 분석하기에 유의미하지 않는 차이를 만들 수 있습니다.
만약 편향을 사용하면 어떻게 될까요?
\[NextLayerinput = Sigmoid(wx+b)\]위의 식을 다음 레이어의 input으로 보내고 b를 평균의 음수인 -8로 가정하겠습니다. 그러면 $X_2$ = [8.4 - 8 , 7.7 - 8 , 8.1 - 8] 로 표현하겠습니다.
\[NextLayerinput = Sigmoid(wx-8)\]$Sigmoid(X_2)$ = [0.5986,0.4255,0.5249] 입니다.
다음 레이어에서 구별 할 수 있을 정도의 값이 등장했습니다. 편차를 사용하지 않을 경우 0.0003 정도의 차이를 가지고 있던 값들은 0.1정도의 유의미한 격차로 표현됩니다.
이것이 바로 활성화 함수를 평행이동 시키는 것입니다.
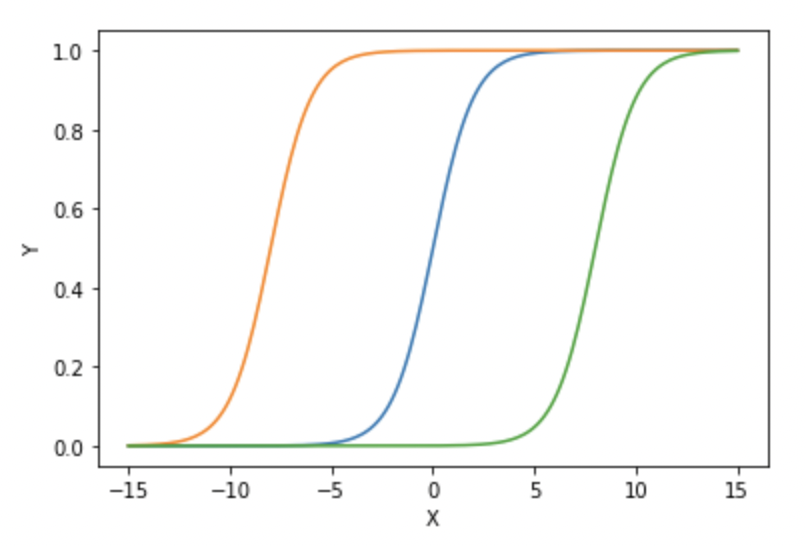
다음의 그림을 확인하면 기존의 활성화 함수( 파란색 )을 평행이동한 경우 동일한 값도 해당 값을 정확히 알 수 있음을 확인 할 수 있습니다.
2. 머신러닝 에러 측면의 편향 (Bias)
정확히 말하면 모델 평가 측면에서의 Bias라고 하는게 맞을 것 같습니다.
단! 활성화 함수가 없는 단순 선형회귀 (예시로 1계층 회귀 레이어)의 경우에는 위에서 다룬 편차(b)가 에러 측면의 편향과 상관성이 있는 것 같습니다.
모델의 결과를 보면 편향과 분산을 알 수 있습니다.
편향은 예측 값에서 실제 값을 뺀 값의 평균이라고 요약 할 수 있습니다. 평균적으로 예측 값과 실제 값이 얼마나 떨어져있는가? 라고 하겠습니다.
분산은 예측 값들이 서로 얼마나 넓게 분포되어 있는지에 대한 값이라고 요약 할 수 있습니다. 분포가 넓을수록 분산은 크다고 말합니다. 예측 값들 사이가 얼마나 넓게 분포되어 있는가? 라고 하겠습니다.
이 중에서 편향이 크다는 이야기는 대체적으로 모델이 간단하다 혹은 학습이 제대로 진행되지 않았다(Under Fitting) 고 말 할 수 있습니다.
왜 학습이 잘 되지 않으면? 편향이 커질까?
두 예측 그래프를 보고 편향과 분산에 대해 알아보겠습니다.
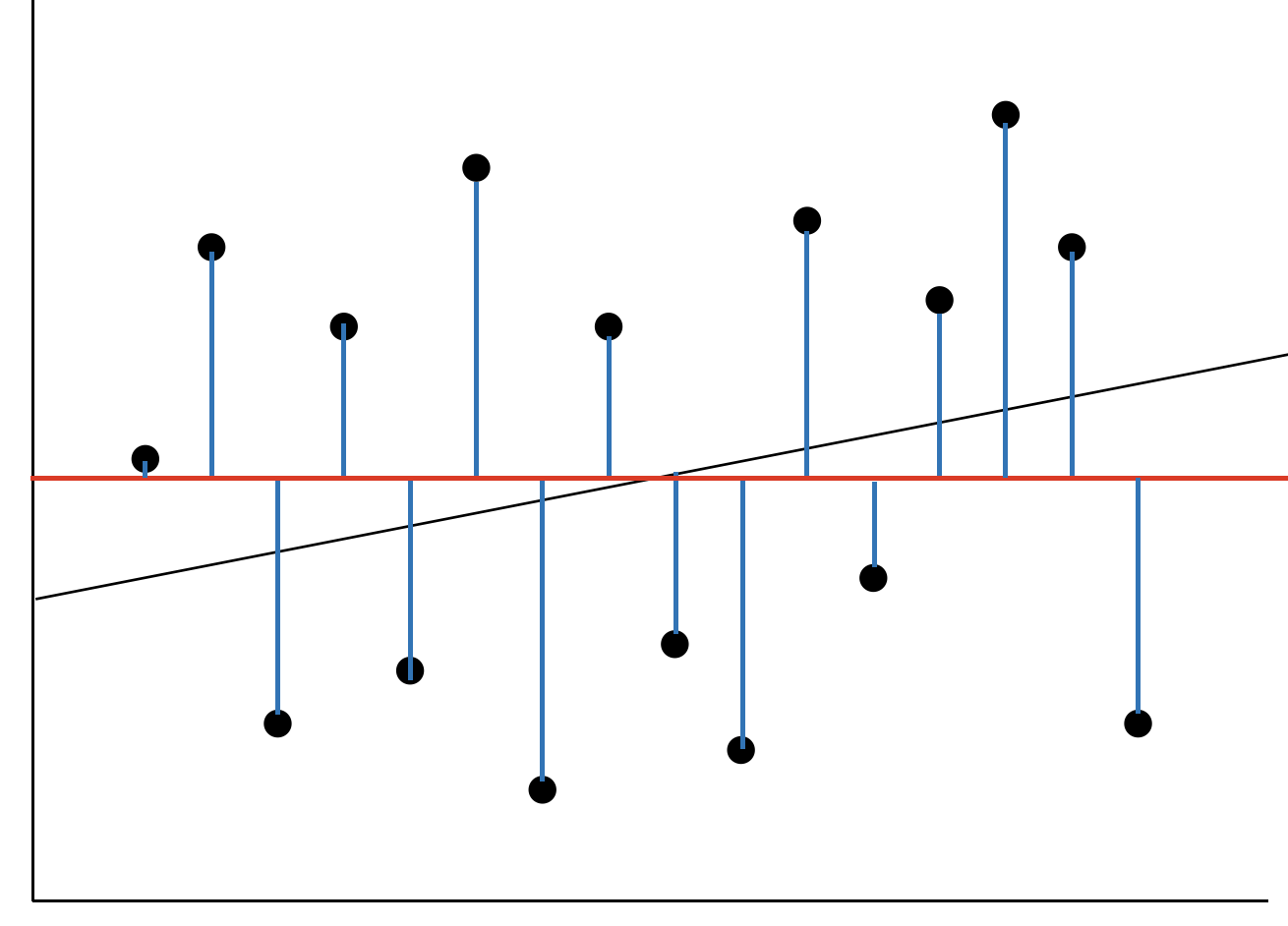
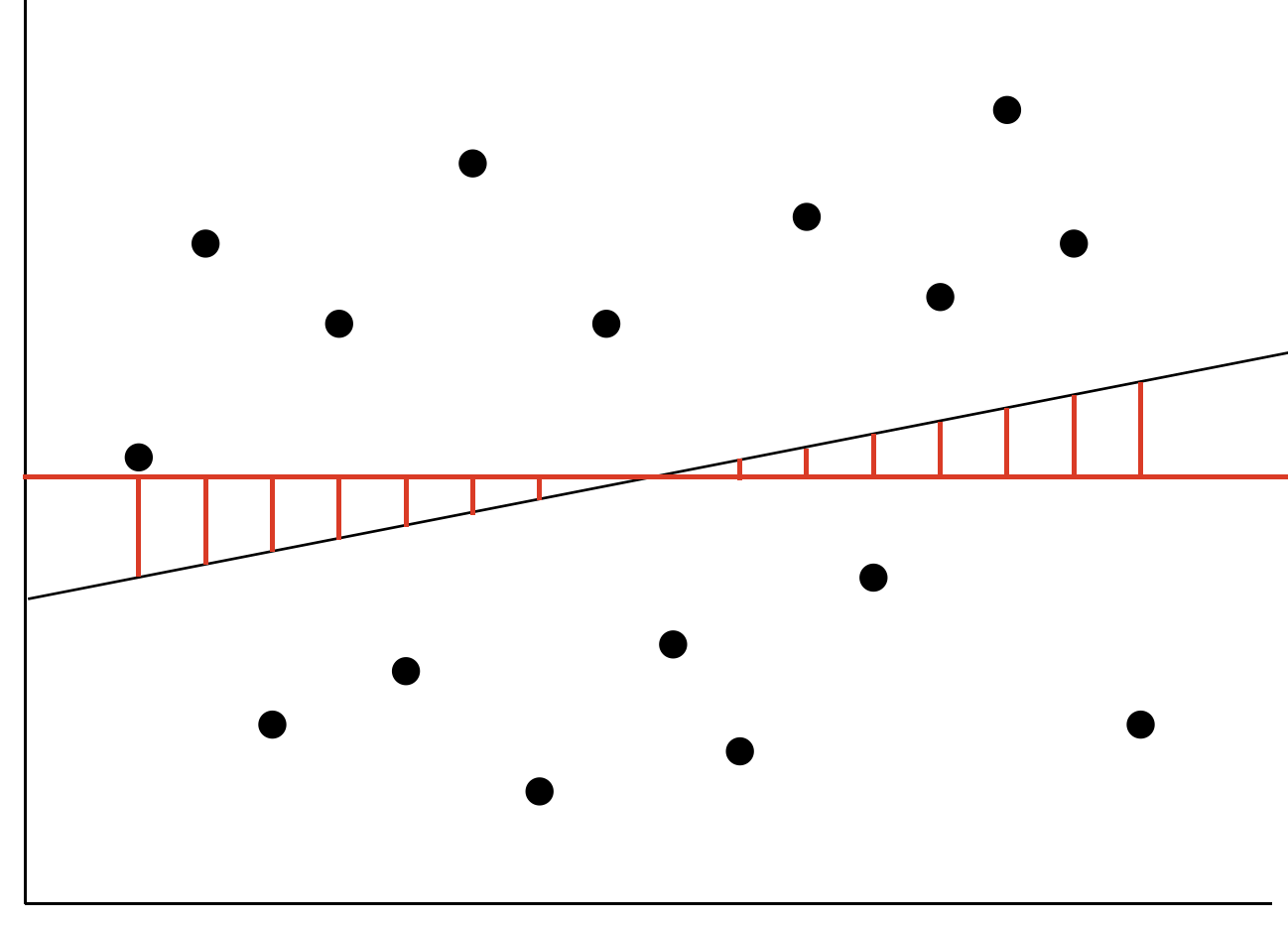
모델 평가에서의 편향은 $(E[\hat{f}(x)]-\bar{f}(x))^2$로 나타 낼 수 있습니다. “실제값이 평균에서 얼마나 멀리 떨어져있는가” 로 요약 할 수 있습니다.
학습이 잘 되지 않은 것은 곧 에러가 크다는 것이며 예측값의 평균과 실제 값의 거리가 크다는 이야기입니다. 또한 모델이 단순하여 유연한 형태의 분류를 할 수 없다는 것을 예상 할 수 있습니다.
위의 1번 그래프를 보면 학습이 제대로 되지 않은 Under Fitting 상태임을 알 수 있습니다. 얼핏 보면 특정 데이터에는 잘 학습 된 것 같지만 MSE를 사용하여 모델을 학습 한다는 가정을 하면 Loss는 제곱을 기반으로 학습되기 때문에 Error는 급격하게 커집니다.
이 그래프에서 편향은 파란선 길이의 제곱의 합이라고 생각 할 수 있습니다.
학습이 진행 될 수록 그래프는 점차 제곱의 합이 작아지는 방향으로 수정됩니다. 가능한 에러가 적은 방향으로 학습이 진행되니까요.
반대의 경우 Over Fitting일 때를 알아봅시다.
그래프 2번을 보면 매우 유연한 모델의 결과를 보실 수 있습니다. 모든 예측값은 정확히 실제 값을 지나며 N 차원의 그래프를 보이고 있습니다. 즉 에러는 0입니다.
이 경우 편향은 가장 최선의 값이 됩니다.
분산은 왜 학습이 잘 될 수록 커질까?
하지만 분산은 반대입니다. 학습이 잘 될 수록 높은 분산을 갖게되죠.
분산을 구하는 식은 $(\hat{f}(x) - E[\hat{f}(x)])^2$입니다. 예측값의 평균에서 예측값은 얼마나 멀리 떨어져있는가? 멀리 분포되어 있는가? 라고 말하겠습니다.
다음의 그래프는 분산 그래프입니다.
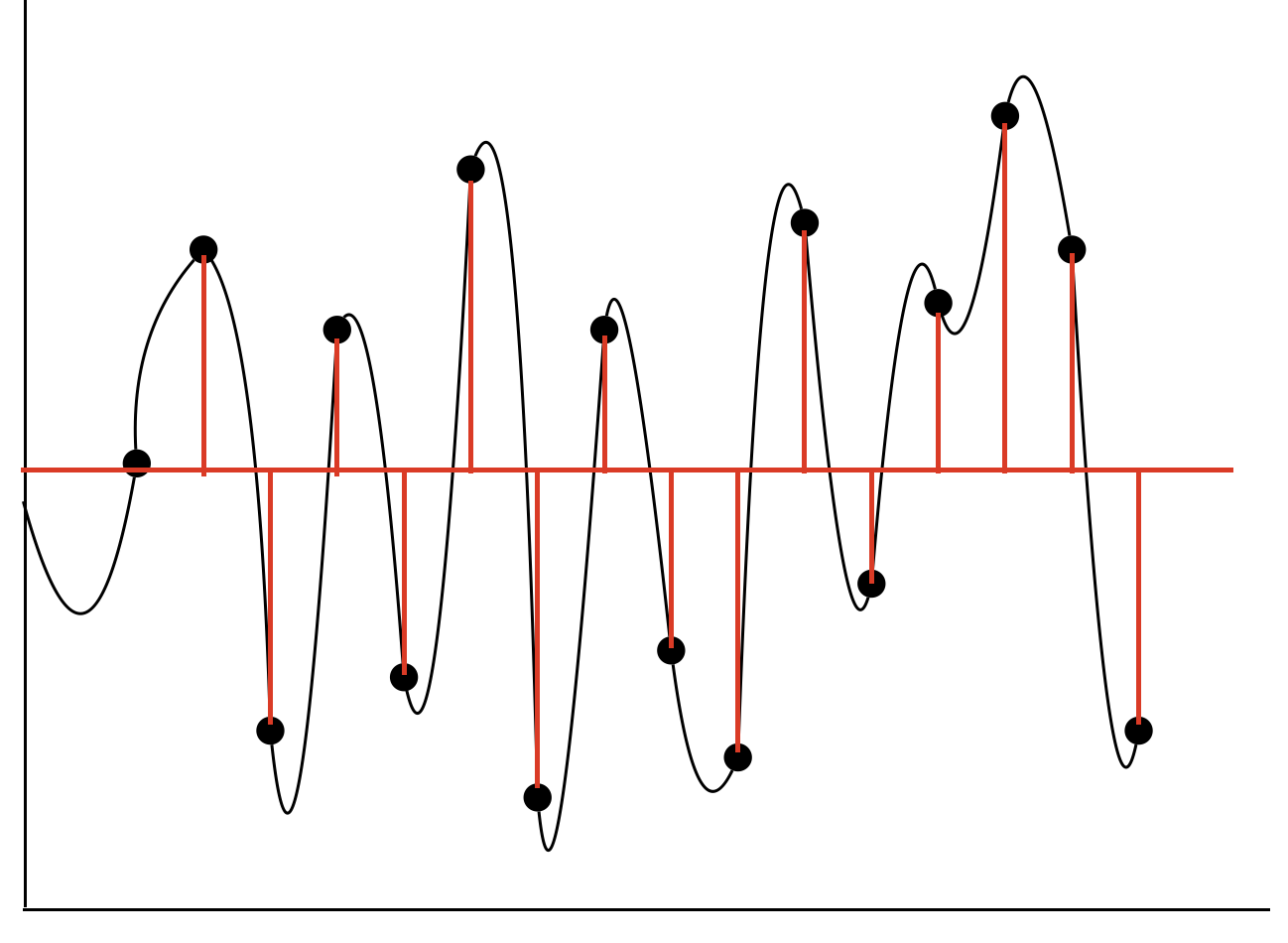
Under Fitting일 경우에는 그래프 1과 같이 예측값과 예측값의 평균이 상대적으로 작을 가능성이 큽니다. 왜냐하면 모델 자체가 유연하지 않기 때문에 데이터의 값에 크게 변형되지 않고 변화가 일정한 편이니까요.
하지만 Over Fitting의 경우에는 모든 예측값이 실제 값과 거의 일치하게 됩니다. 그 결과 모델은 복잡해지고, 데이터에 따라 큰 변화량을 갖게 되어 예측값이 크게 차이가 생깁니다. 위의 두 그림으로 간단하게 알아 볼 수 있을 것 같습니다.
편향과 분산은 Trade-Off 관계이다.
Under Fitting 일 수록 편향은 커지고 분산은 작아집니다. Over Fitting 일 수록 편향을 작아지고 분산은 커집니다. 두 지표 모두 작으면 작을수록 좋은 지표이지만, 둘 다 완벽한 모델을 만드는 것은 불가능에 가까우니 우리는 선택을 해야합니다.
어느 지점에서 만족할것인가
우리는 Over Fitting을 두려워하며 Under Fitting을 벗어나는 방법을 찾아서 이러한 Trade-Off 관계에서 그나마 최선의 결과를 도출해야 합니다.