꾸준함이 중요한 Lion2me의 기술블로그

선형 회귀 분석

13 Jun 2021

선형 회귀 분석

데이터 분석 교과 과정을 수강하면서 회귀분석 중 계수를 추정하는 점수에 대해 이해가 부족하다는 사실을 깨닫고 늦게나마 관련 공부를 했습니다.

선형 회귀 분석이란

회귀 분석이란 관측한 특징 X를 기반으로 해당 특징이 결과에 미치는 영향의 정도에 대해서는 가중치 W로 가정하여 문제를 해결하는 방법입니다.

여기서 선형이라는 단어는 공부한 바로는 특징과 예측값의 그래프 자체가 선형 관계라는 뜻이 아닌 가중치에 해당하는 W가 선형적인 특징이 있다는 것으로 이해하고 있습니다.

선형 회귀 분석

실제로 테스트 하면서 알아보겠습니다.

단순한 선형 회귀를 보여주는 그래프는 다음과 같습니다. 문제에 대해서 특징 x의 값에 대해 예측값 y_hat과 실제 정답인 y의 오차가 가장 적은 선을 그리는 것이 목표입니다.

이 말만 들으면 뭔가 이해가 안되니 공식을 사용해봅시다. 먼저 선형적인 관계를 나타내는 1차 함수를 정의해봅시다.

\[\hat{y} = wx + b\]

그리고 동일한 데이터가 주어졌을 때의 각각의 데이터를 공식에 넣어보겠습니다.

\[0 = 0w + b\] \[2 = 1w + b\] \[4 = 2w + b\] \[5 = 3w + b\]

두 번째 공식까지는 w값과 b값을 쉽게 추정할 수 있습니다. w가 2이며 동시에 b가 0이라면 두 공식은 완벽히 정답에 일치하게 됩니다. 하지만 마지막 공식에서 이 추정은 무너지게 되죠, 세 번째 공식에서 동일한 w와 b값으로 연산을 하게 되면 예측한 h_hat은 6이 됩니다.

그러면 오차를 구해봅시다. 오차를 구하는 방법은 사실 다양한 방법이 있습니다만, 주로 사용하는 오차는 MSE(Mean Square Error)입니다. 공식으로 적으면 다음과 같습니다.

\[MSE = {1\over{n}} \sum_{i=1}^{n}({y_i - \hat{y_i}})^2\]

정답과 예측한 예측값과의 차를 제곱한 값을 모두 더한 뒤 데이터의 수로 나누어 주면 에러를 알 수 있습니다. 통계학적으로 데이터의 수로 나누어주는 것은 즉 수 많은 모수에서 관측한 표본의 수를 다루는 것이기에 n-1로 나누기도 합니다만, 어차피 오차를 얻기 위함이며 변동하는 값이기에 신경쓰지 않아도 될 듯 합니다.

그러면 오차를 줄여보도록 하겠습니다. 우리는 이 학습 과정에서 알아야 할 개념이 있습니다. 조금 더 깊은 내용에 대해서는 이후에 또 다른 포스트에서 다루도록 하겠습니다만 Gradient Descent를 통해서 우리는 w값이 이동함에 따라서 오차(Loss)가 얼마나 증감하는지 기울기를 통해 예측할 수 있습니다.

일단 짧게 “w값의 변화로 인한 오차(Loss)가 얼마나 영향을 받을지에 대해 그래프의 기울기를 통해 어느정도 예측 할 수 있다.” 로 줄이겠습니다. 말 그래도 어느정도만 예측 가능합니다. 참고로 해당 글에서는 앞으로 Loss를 사용하겠습니다. 엄밀히 말하면 오차와 Loss는 차이가 있습니다. 오차는 관측값과 정답에 대한 차이값에 대해 통합적으로 나타내는 말이지만 Loss는 정해진 Loss Function에 따라 달라지는 값이라고 배웠습니다. 아닐 수 있습니다

그러면 우리는 Loss가 적어지는 방향으로 학습을 진행합니다.

다시 그래프로 돌아가보겠습니다. 두 번째 공식까지만으로 그려진 그래프를 해당 데이터의 위치에 맞게 선을 그러보면 다음과 같은 그림이 됩니다.

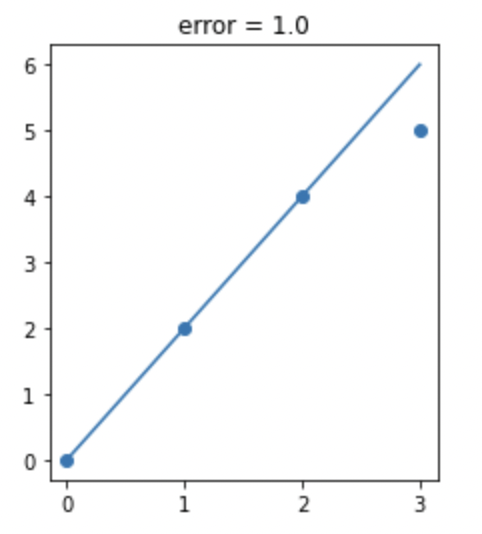
그러면 오차가 발생하죠, 세 번째 데이터와 그래프 위의 회귀 선은 1의 오차가 있고 MSE 값으로 보면 3분의 1의 Loss가 발생합니다.

Loss를 줄이기 위해 w값을 수정해보겠습니다. 다음은 w(기울기)를 수정한 그래프 입니다.

import matplotlib.pyplot as plt
import numpy as np
from functools import reduce

x = [0,1,2,3]
y = [0.0,2.0,4.0,5.0]

line_y = [[0.0,2.0,4.0,6.0],[0,1.9,3.8,5.7],[0,1.8,3.6,5.4],[0,1.7,3.4,5.1]]

f, axes = plt.subplots(1, 4, sharex=True, sharey=True)
f.set_size_inches((16, 4))

for i in range(0,4):
    axes[i].scatter(x,y)
    axes[i].plot(x,line_y[i])
    error = reduce(lambda err, cur : err + (cur[0] - cur[1])**2 , zip(y,line_y[i]) , 0 )
    axes[i].set_title("MSE = "+str(error/4)[:5])

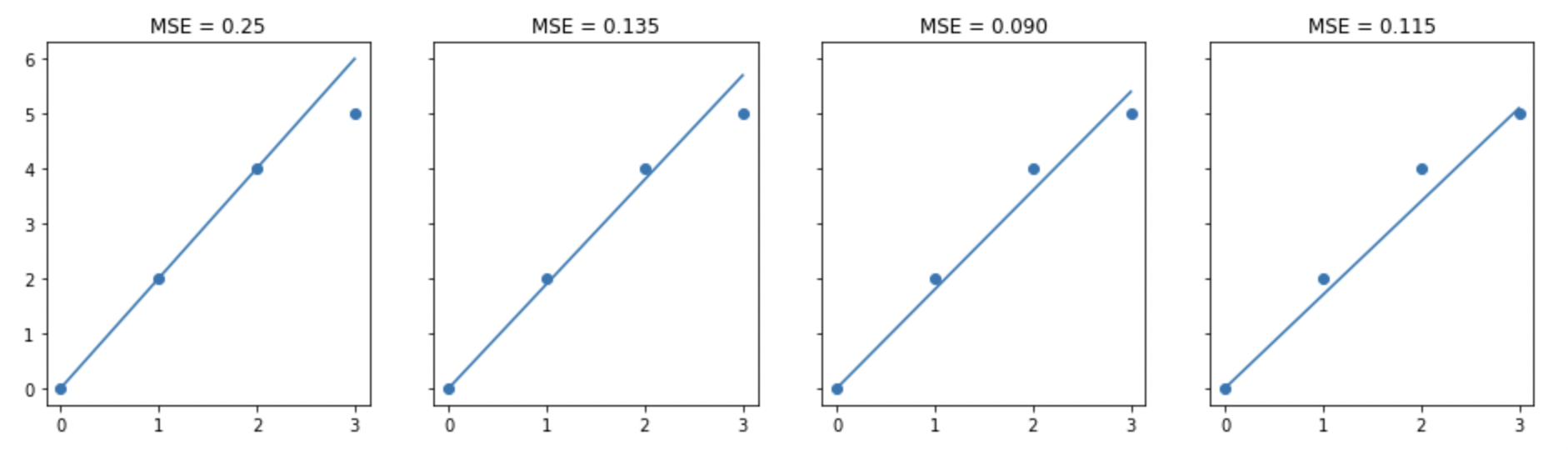
그래도 이상한 점이 있습니다. 바로 이해하셨겠지만 모든 선이 0을 지나가게 되면서 그릴 수 있는 그래프의 한계가 명확한 점이 보이실겁니다. 이때! 우리의 b(편향)이 일을 시작합니다.

두 그림의 차이를 보시면 왜 편향이 중요한 지 알 수 있습니다.

우리는 b값도 학습에 따라 바뀌는 값 임을 알 수 있습니다. 그러면 공식을 바꾸어서 나타내는게 더 이해가 빠를 것 같습니다.

\[\hat{y} = \beta_0 + \beta_1x_1\]

똑같은 1차 방정식이지만 우리가 찾아야 할 값이 2개임을 나타냈습니다. MSE의 공식도 다음과 같이 수정 할 수 있습니다.

\[MSE = {1\over{n}} \sum_{i=1}^{n}({y_i - \beta_0 - \beta_1x_1})^2\]

그리고 특징 $x$의 갯수가 $k$개 일 경우에는 다음과 같이 공식을 일반화 시킬 수 있습니다.

\[MSE = {1\over{n}} \sum_{i=1}^{n}({y_i - \beta_0 - \beta_1x_1} - \beta_2x_2 ... \beta_kx_k)^2\]

우리는 이 값이 최소화되는 $\beta$를 찾으면 가장 데이터를 잘 나타내는 선형 방정식을 구할 수 있습니다.

마지막으로 최적의 $\beta_0$과 $\beta_1$을 찾게 되면 다음과 같은 그래프를 그릴 수 있습니다.

line_fitter = LinearRegression()
line_fitter.fit(np.array(x).reshape(-1,1), y)
y_predicted = line_fitter.predict(np.array(x).reshape(-1,1))

print('coef = ',line_fitter.coef_)
print('intercept = ',line_fitter.intercept_)
print('y_predict = ',y_predicted)

plt.scatter(x,y)
plt.plot(x,y_predicted)

error = reduce(lambda err, cur : err + (cur[0] - cur[1])**2 , zip(y,y_predicted) , 0 )
plt.title("MSE = "+str(error/4)[:5])

# y = 1.7x + 0.200

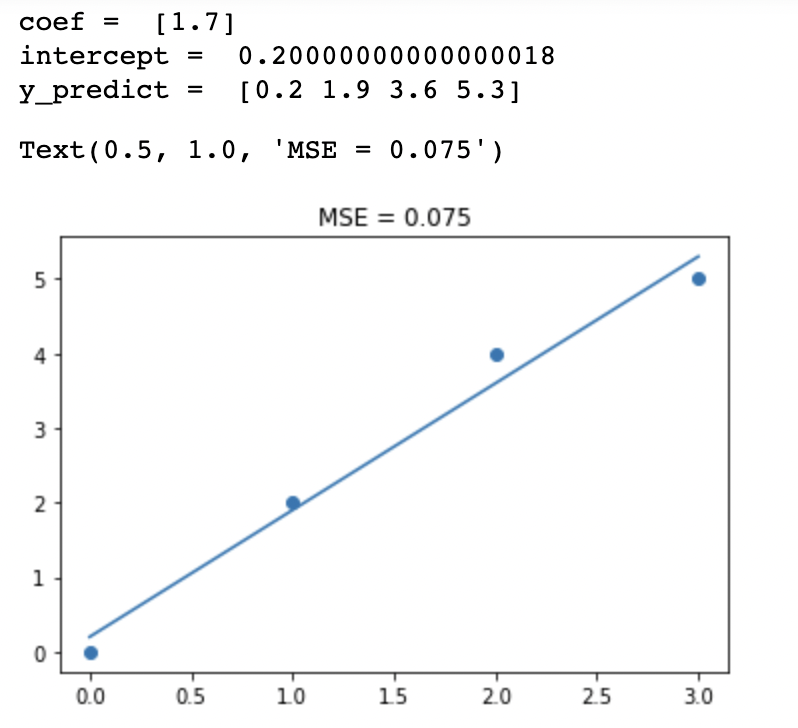
위의 그림은 편향도 학습하여 Loss를 최소화 시킨 그림입니다. 확연히 Loss가 줄어든 것을 확인할 수 있습니다. 이 그림에서는 눈에 띄지 않더라도 데이터가 많아지면 더욱 더 눈에 띄는 차이를 알 수 있습니다.

선형 회귀 분석을 진행 할 때 주의할 점

선형 회귀는 해당 특징이 가진 가중치를 얻는 방법이기에 사용할 때 명심해야 하는 점이 있습니다.

1. 특징(독립변수)는 정말 독립적인가?

특징은 그 자체로써의 특징을 가지고 있어야 합니다. 예를들어 다음과 같은 특징이 있을 경우 선형회귀는 좋은 특징을 학습하지 못할 수 있습니다.

점수과 등급 - 등급은 점수에 따라 높게 책정됩니다. 즉 당연히 점수가 높은 사람은 등급이 높게 책정되며, 이 경우에는 올바른 가중치를 갖지 못할 가능성이 있습니다. 즉 특징으로써 가중치를 신뢰 할 수 없습니다. 이 경우에는 두 특징 중 하나만을 사용하도록 혹은 두 값을 더하는 방식을 이용하여 사용하도록 해야합니다.

독립변수간의 상관관계가 있는지를 판별하기 위해서 우리는 다중공선성을 이용하여 판단할 수 있습니다.

이런 특징을 파악하려면 특징들간의 선형관계를 확인해보면 어느정도 알 수 있다는 것으로 알고 있습니다.

2. 문제가 선형적인가?

문제 자체가 선형적이지 않는 문제들이 있습니다. 이 경우에는 고차원의 복잡한 모델로 학습을 하더라도 문제에 맞는 모델이 만들어지지 않을 경우가 있습니다. 물론 매우 고차원의 모델을 사용하면 학습이 가능할 수 있지만 과적합의 위험이 높아지게 됩니다.

3. 문제를 해결하기 위한 특징은 충분히 수집되었는가?

선형회귀의 공식에는 특징과 특징이 가지고 있는 가중치의 곱들의 합이 포함되어 있으며 동시에 찾지 못한 특징에 대해 판단하기 위해 상수를 더하는 과정이 포함되어 있습니다. 즉, 현재 관측한 특징으로 설명되지 않는 다른 특징이 있을 것이라는 가정이 포함되어 있습니다.

입실론 혹은 편차 라고 부르는 이 상수가 우리에게 말해주는 바는 관측된 특징과 그에 대한 가중치만으로 설명되는 분산(학습으로 줄일 수 있는 오차) 와는 다르게 학습을 하더라도 줄일 수 없는 오차가 있다는 점을 시사합니다.

만약에 특징의 갯수에 비해서 데이터 수가 너무나 적거나 혹은 특징이 문제를 해결하기에 좋은 특징이 아닐 경우에는 이 상수가 커짐으로써 우리는 문제에 대해 좋은 모델을 만들 수 없습니다.

실제로 확인해보자

테스트에 사용한 데이터는 집 값 데이터를 이용해보겠습니다. 데이터는 BaekKyunShin 님의 깃허브에서 가져왔습니다.

BeakKyunShin님께서 분석한 내용을 참고해서 간단히 분석해보겠습니다.

import pandas as pd
import seaborn as sns
from patsy import dmatrices
import statsmodels.api as sm;
from statsmodels.stats.outliers_influence import variance_inflation_factor
%matplotlib inline

df = pd.read_csv('./house_prices.csv')
df.head()
df.describe()

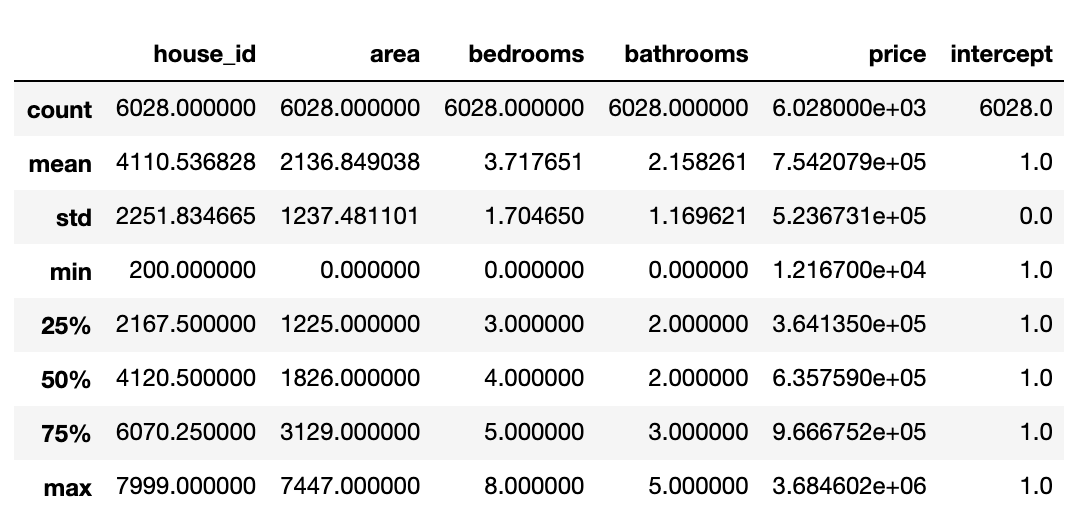
데이터 상태를 보니 이웃에 대한 점수와 집의 스타일에 대한 데이터는 카테고리 형태로 이루어져 있으니 일단은 분석의 범주에서 제외하고 추후에 완성된 모델에서 사용하도록 하겠습니다.

df['intercept'] = 1
lm = sm.OLS(df['price'], df[['intercept', 'bedrooms', 'bathrooms', 'area']])
results = lm.fit()
results.summary()

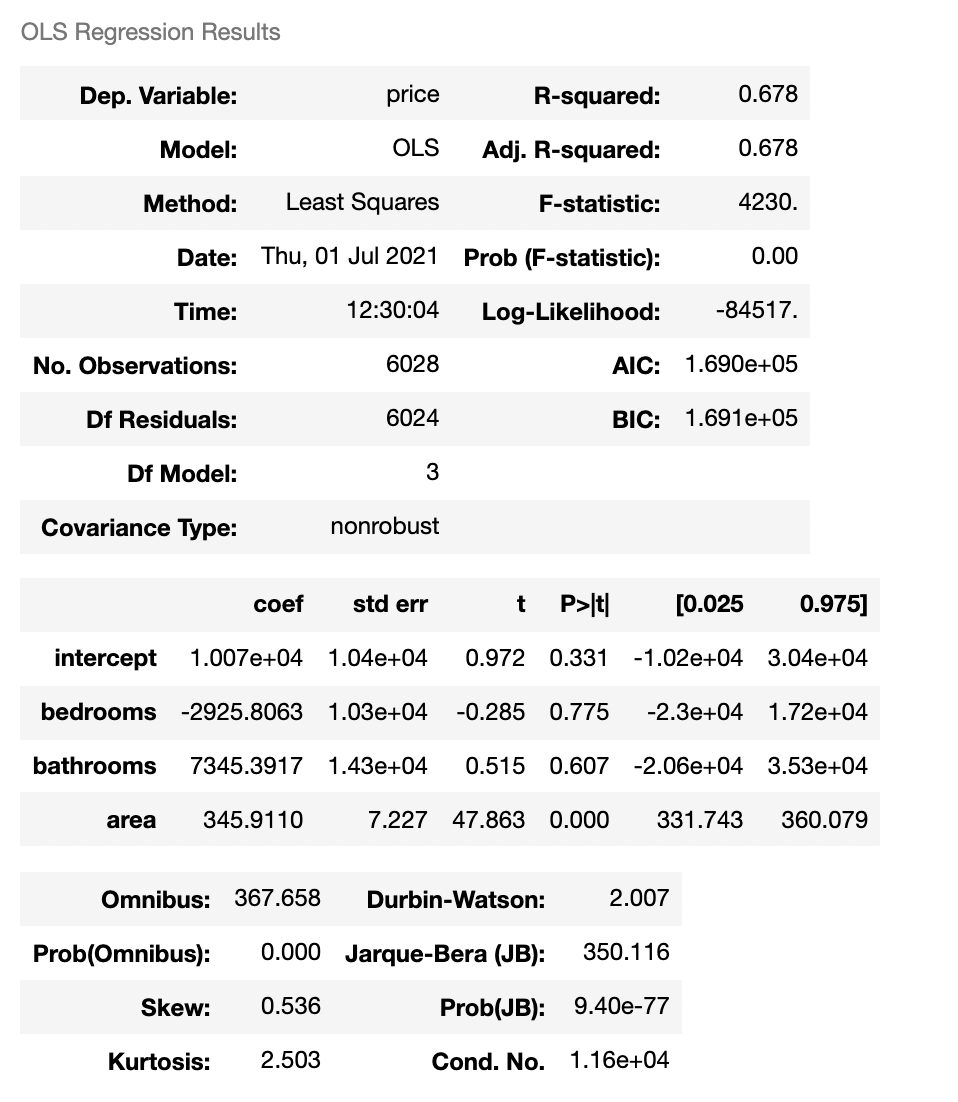
위의 분석표는 방의 개수 / 화장실의 개수 / 면적을 이용하여 집 값과의 관계를 분석한 결과입니다.

먼저 결정계수 R-squared를 보면 0.678입니다. 이 결정계수는 현재 독립변수는 종속변수인 집 값에 대해 0.678정도 표현할 수 있다는 추정치는 알려주고 있습니다.

주로 선형회귀 분석을 할 때 분산과 편향을 기반으로 분석을 진행하며 결정계수는 선형회귀의 적합도를 나타내는 지표로 사용되고 있습니다. 예측값에 대한 분산을 기반으로 구하는 것으로 이해하고 있습니다만, 추가적으로 공부하겠습니다.

결정계수는 0부터 1까지의 수를 가지며 0에 가까울수록 해당 선형회귀는 적합하지 않다는 뜻이며 1에 가까울수록 적합한 선형회귀입니다. 단 극단으로 1에 가까우면 데이터의 수가 너무 적은게 아닌지 검증을 해 볼 필요성이 있다고 조심스럽게 의견을 제시해봅니다.

또 하나 중요한 것은 intercept 부분입니다. 두 번째 표를 보면 실제로 분석을 한 요소가 아닌 요소로 슬쩍 끼어있는 것을 볼 수 있습니다.

이것은 우리가 아직 찾지 못한 특징입니다. 중요하니까 한번 더 적겠습니다 우리가 아직 찾지 못한 특징입니다.

거의 모든 모델이 완벽할 수 없는 이유인 intercept는 모델이 가진 한계점입니다.

집 값을 정하는 요소가 과연 방의 갯수 혹은 화장실의 갯수, 땅의 면적이라고 단정지을 수 있을까요? 그렇다면 저는 지방 지역과 10배에 가까운 집 값을 가진 서울에 대해서 전혀 해석 할 수 없을 것입니다.

혹시 우리가 해당 데이터를 조금 더 깊게 분석하기 위해 -편향을 줄이기 위해- 더 많은 데이터를 수집해보겠습니다. 예를 들면 대형마트와의 거리 / 대형병원과의 거리 / 여러 기피시설과의 거리 데이터를 모두 수집했다고 하겠습니다.

수집한 데이터가 집 값에 영향을 끼치는 유의미한 관측치라면 데이터를 더 잘 설명할 수 있게 되고, 모델은 더욱 유연한 그래프를 그리게 됩니다. 동시에 설명할 수 없는 값인 편향은 감소하게 됩니다.

독립적이지 않는 특징으로 분석하는 결과 ( 가중치의 차이 값 )

위의 문제에서 이상한 점을 하나 발견할 수 있습니다. 바로 두 번째 표에 등장한 bedrooms의 가중치입니다. 그대로 해석한다면 침실의 개수가 많아질수록 집 값은 감소한다. 이상합니다.

우리는 두 가지 방법을 이용해서 다중공선성을 확인할 예정입니다. 바로 VIF와 상관계수입니다. 사실 VIF만 이용해도 괜찮습니다.(더 정확할거에요)

독립변수들을 scatter 그래프로 표현해보겠습니다.

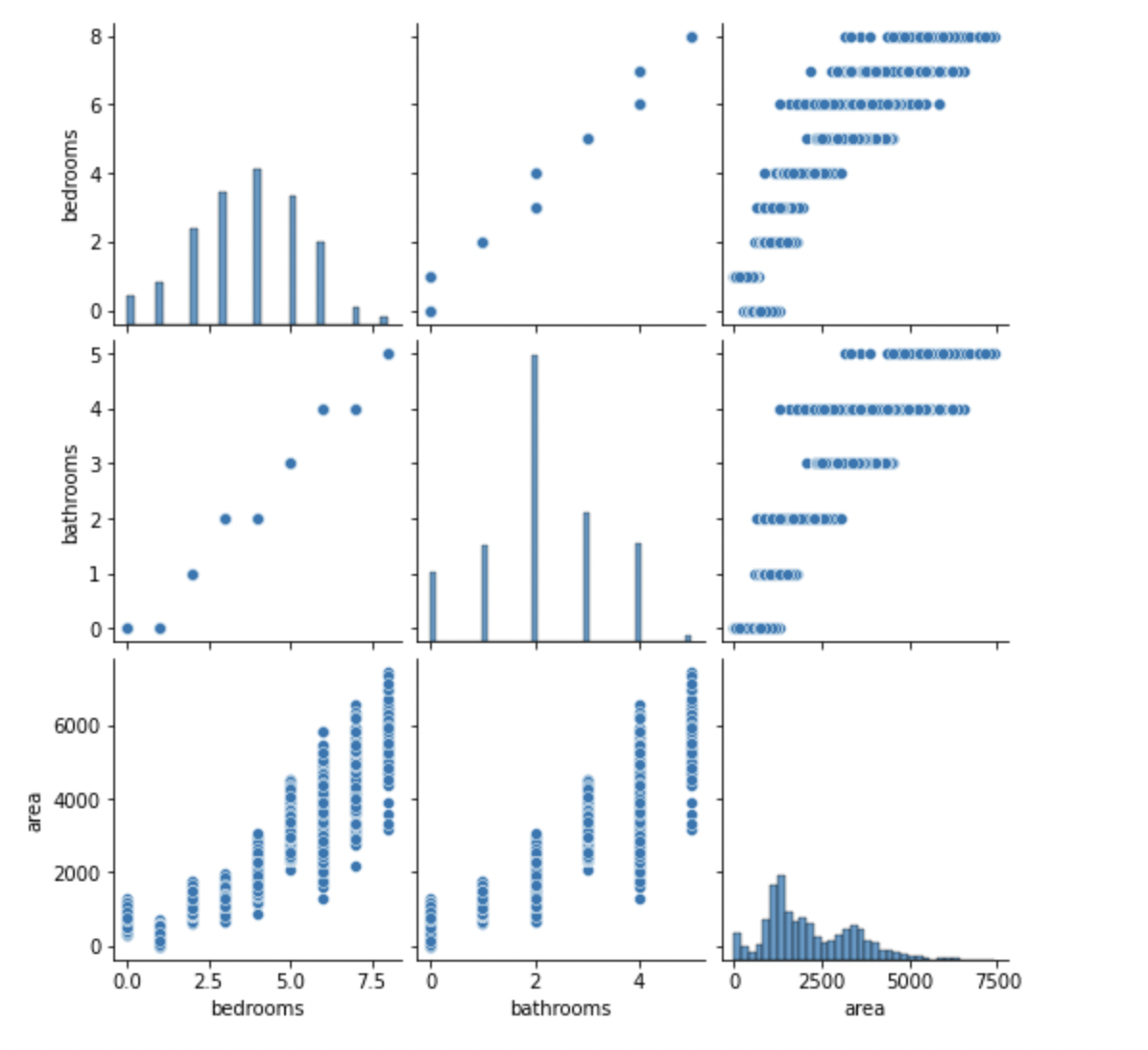
선형적이지 않는 데이터를 분석한 결과

추가예정

문제를 해결하기 위한 특징이 부족한 결과 ( 그래프 자체가 무의미 )

추가예정

참고

https://heung-bae-lee.github.io/2020/01/04/machine_learning_01/

https://woochan-autobiography.tistory.com/135

https://todayisbetterthanyesterday.tistory.com/8

https://agronomy4future.com/2020/10/27/회귀분석의-결정계수-r-squared-를-가장-쉽게-설명해-보자/