강화학습의 시작
좋은 기회를 통해 강화학습에 대한 기초를 공부하게 되어 블로그에 남깁니다.
강화학습은 흔히 말하는 AI 스스로 판단하여 가장 좋은 방법을 찾아나가는 진정한 의미의 인공지능이라고 볼 수 있는 기술입니다. 여기까지 말하면 터미네이터와 같은 공상 영화의 한 장면을 연상할 수 있지만 사실은 최고의 효율을 얻기 위한 시도를 통해 다음 행동을 판단하는 하나의 방법입니다.
대부분의 강화학습은 MDP(Marcov Dicision Process)를 이용합니다. 어렵게 생각할 수 있지만 이전 상태가 다음 상태에 영향을 준다라고 이해하면 될 것 같습니다. 이전에 포스팅한 Marcov Model과 비슷합니다.
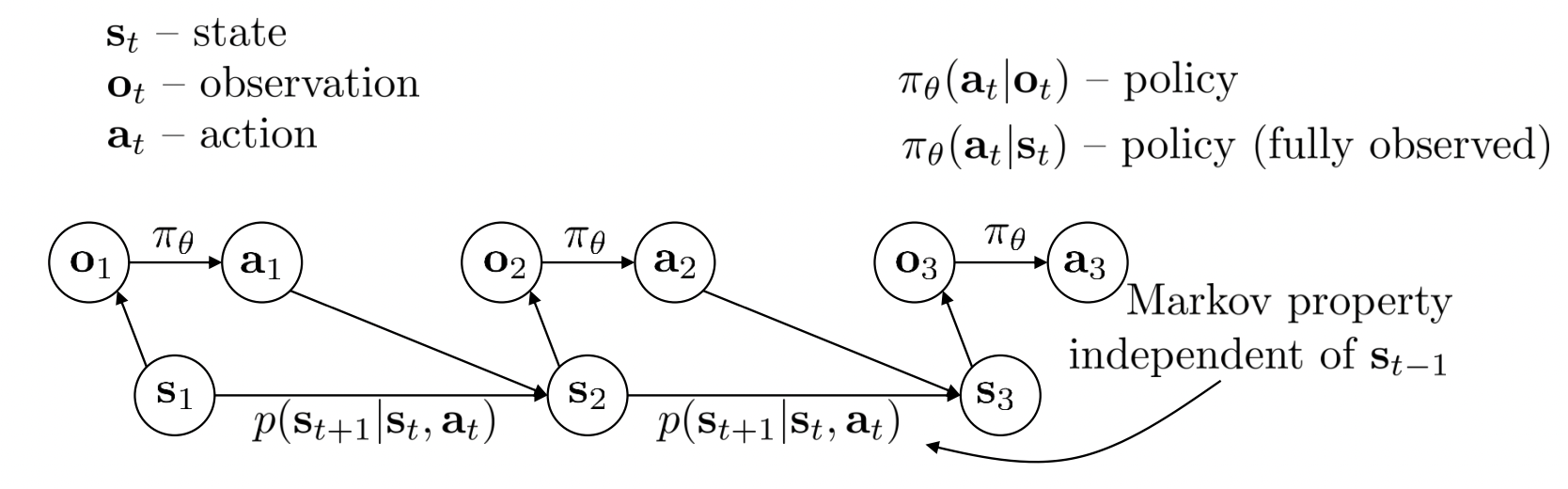
위의 그림은 cs285 강의에서 참고해서 가져왔습니다.
그림에는 총 3개의 파라미터가 있습니다. 상태 $s$와 행동 $a$ 그리고 관측 값인 $o$ 입니다.
화살표가 가리키는 대로 $a$와 $s$를 공식으로 표현해보면 $\pi_\theta(a_t |o_t)$ $p(s_{t+1} |a_t,s_t)$ 이렇게 표현할 수 있습니다. Marcov Process의 특성 상 확률로 표현되어 있으며 어렵게 느껴지겠지만, $a_t$는 $o_t$의 영향을 받는다. $s_{t+1}$은 $s_t$와 $a_t$의 영향을 받는다. 정도로만 이해해보죠.
그런데 관측 값의 경우에는 어떻게 표현할 수 있을까요? 관측 값은 어디까지나 상태 $s$에서 관측 된 정보입니다. 즉 상태 $s$에서 관측 된 값이므로 $s$의 영향을 받습니다. 그렇다면 $\pi_\theta(a_t |o_t)$를 $\pi_\theta(a_t |s_t)$라고 표현 할 수 있지 않을까요? 어차피 $o_t$가 $s_t$로 표현 될 수 있으니 말이죠. 관측 값이 아예 없다면 문제가 되겠지만, 현재 상태의 관측 값이 없다면 어떻게 될까요? 학습이 끝날지 탐험을 할 지 조금 더 공부해보겠습니다.
여기서 의문이 생깁니다. 그러면 $s_{t+1}$의 확률은 $s_{0 … t}$와 $a_{0 … t}$ 모두의 영향을 받는 걸까요? 맞는 말입니다만, 공식이 $p(s_{t+1} |s_t,s_{t-1} … s_{0})$ 이런식으로 전개되지 않습니다. 왜냐하면 $p(s_{t})$는 $s_0$부터 $s_{t-1}$까지의 특징을 가지고 있음을 가정하기 때문입니다. 그렇기 때문에 $p(s_{t+1} | s_t,s_{t-1},s_{t-2}…s_0 ,a_{t}…)$는 결국 $p(s_{t+1} |s_t,a_t)$와 같습니다. 이 점은 중요한 특징이기에 기억해주시길 바랍니다.
다시 그림을 보겠습니다.
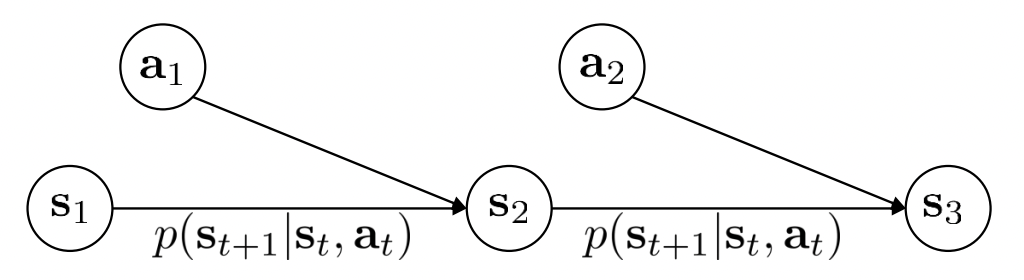
우리는 여기서 [행동에 대한] 학습 정책(Policy) 와 상태의 전이(Transition)를 따로 표현해보겠습니다.
Policy
$policy = \pi_\theta(a_t |s_t)$
Policy는 상태 $s_t$에서 행동 $a_t$를 수행 할 확률입니다. 정확히는 상태 $s_t$에서 어떠한 행동($a_t$)을 할 것인지 정하는 것 입니다.
그리고 우리가 찾고 싶은 값 또한 이 Policy입니다. 이 부분의 이해는 간단한 예시만으로도 이해하기 쉬운데, 우리는 A라는 상황에서 어떤 행동을 할 것인지를 알고 싶습니다. 예를 들면 리그오브레전드에서 한타가 일어났을 때 현재 상황($s$)에서 어떤 스킬($a$)을 사용 할건지 알고 싶습니다. 현재 상황이 $s_t$라면 스킬(행동) $a_t$을 수행하는 것에 대해 알고 싶은거죠. 그래서 우리는 Policy를 알아내야 합니다.
Transition
$transition = p(s_{t+1} |s_t,a_t)$
상태 $s_t$에서 액션 $a_t$를 수행하여 상태 $s_{t+1}$로 전이 될 확률입니다. $s_t$와 $a_t$를 알고있다면 $s_{t+1}$은 하나의 환경입니다. 상수와 같이 고정적이라고 할 수 있을 것 같습니다.
강화학습의 목표
강화학습의 목표는 너무나 명확합니다. 바로 Maximum Reward 입니다. 더 정확히 말하면 Reward의 합의 최대입니다.
우리는 하나의 상태에서 어떠한 행동을 할 지 정하고 행동하여 다음 상태의 정보를 얻습니다. 그 과정에서 우리는 상태 혹은 다음 행동으로부터 얻을 수 있는 Reward를 알 수 있습니다. 그 Reward의 합이 가장 큰 Path를 찾아가면 우리는 정답에 가까운 Path를 알 수 있습니다.
하지만 명확한 행동이 정의되지 않는 문제도 있습니다. 예를 들면 몬스터와의 접촉을 회피하는 문제는 어떨까요? 만약 0도부터 180도까지의 회전 각도 중 화면상의 모든 몬스터의 접촉을 피하기 위한 최선의 각도와 이동 거리를 구하는 문제라면?
우리는 회전 각도를 0도부터 180도까지 n도를 기준으로 세분화하지 않았습니다. 그렇기 때문에 문제는 이산확률이 아닌 연속확률 문제가 되어버렸죠.
행동의 개념이 연속확률로 변해버린 이상 우리는 1번 액션, 2번 액션이 아닌 연속확률분포상의 특정 지점의 가능성을 구해야합니다.
9.3도(현재 각도)에서 11.6도 회전하고 20.8cm(현재 위치)에서 22.1cm까지 이동했을 경우의 최대 Reward를 구하는 문제는 어떨까요? 상태(9.3도)와 액션에 따른 Reward를 구하는 과정은 명확하네요.
이렇듯 우리는 Policy에 따라 학습을 진행하며 Transition에 따라 상태는 변화합니다. 이 방식을 바탕으로 강화학습의 종류에 대해 공부해보겠습니다.
강화학습은 크게 2가지로 나눌 수 있습니다.
바로 Value Based 방식과 Policy Based입니다.
Value Based
Value Based는 상태 s에서 행동 a를 시행했을 때의 결과(Reward)를 $r(a_t |s_t)$ 값으로 저장해놓는 방법입니다.
Value Based에서 명심 할 점은 기본적으로는 Greedy한 형식을 따른다는 것입니다. 그래서 가장 정답에 가까운 Path를 얻기 위해 기록과 탐험을 반복하며 결국에는 최선의 Path를 특정 짓습니다.
위의 설명에서 나오는 이산적인 분석에서 사용 될 수 있는 방법이죠.
Value Based는 결국 현재 상태 혹은 다음 행동으로부터 얻을 수 있는 Reward의 합을 최대화하는 방법입니다. 이 두 가지를 구분하여 설명해드리겠습니다.
상태 가치 함수 (State Value Function)
상태 가치 함수는 현재 상태($s_t$)에서 기대되는 Reward의 합을 알 수 있는 방법입니다. 상태에 대해서 검증할 수 있는 방법이라고 말할 수 있겠습니다. 간단히 말하자면 가장 효과적인 방법으로 학습이 진행된다면 해당 상태에서 앞으로 진행되는 과정을 통해 얻어지는 Reward의 합은 최대가 될 것입니다.
$s_t$ 상태에서의 Reward의 합을 $G_t$라고 하겠습니다. 여기서 사실 $R_{t+1}$부터 시작하는 것이 좀 더 정확한 표현이지만, 식의 편의를 위해 $R_t$로 적겠습니다.
\[G_t = R_{t} + R_{t+1} + R_{t+2} + R_{t+3} + R_{t+4} ... R_{fin}\]행동 가치 함수 (Action Value Function)
행동 가치 함수는 상태($s_t$)에서 행동($a_t$)을 취했을 때 기대되는 Reward의 합을 알 수 있는 방법입니다. 해당 상태에서 다음 취할 행동에 대해 검증하는 방법으로 사용 될 수 있습니다.
Policy Based
Policy Based의 경우에는 상태 s에서 행동 a를 시행하면서 얻는 Reward의 합을 최대화하게끔 $\theta$를 최적화합니다.
[ 미완미완미완 더 추가해야합니당 ]